Introduction

The subject of elementary particle physics to have begun with the discovery of the electron more than century ago. In the following 50 years, one new particle after another was discovered, mostly as a result of experiments with cosmic rays, the only source of very high energy particle then available. After second war the accelerator technique was used to study the elementary particle physics. Nuclear and particle physics are essentially at the forefront of nowadays understanding of physics. Nucleus is a bound system of strongly interacting protons and neutrons. Unfortunately, modern QCD does not provide us with the tools to calculate the bound states properties of the proton (deuteron) from first principles [1].

In this connection the new experimental data about strong nuclear interaction are very valuable. The present paper is devoted to the results of measurements of residual strong nuclear interaction via the study the low-temperature optical spectra (reflection, photoluminescence) of the LiH (without strong interaction in hydrogen nucleus) and LiD (with strong interaction in deuterium nucleus) crystals which differ by term of one neutron from each other. We should repeat that nowadays in textbooks and elsewhere the separation of electromagnetic and strong interaction is tacitly assumed. It is very strange because up to present time we do not even know the strong nuclear force very well. The origin of the strong interaction is very important especially in the problem of all force unification [2-4].

The results of the paper have shown a new light on some residual strong nuclear interaction (ultimately based in the character of magnetic forces, the electromagnetic or color origin, which by their very nature, are difficult to conceal within the elusive nucleon physical boundary) between both kind of forces which experimentally manifested through isotopic shift of zero phonon line in optical spectra [5].

As indicated above, there is a common place in SM of modern physics that the strong force does not act on leptons [6] (Figure 1).

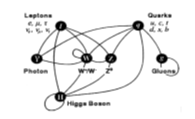
Figure 1: Summary of interactions between particles described by the Standard Model.

Following this conclusion, we do not must to observe the dependence of the optical properties of solids on addition neutrons in substance. This contradicts the history of the development of isotope effect. The first attempt to discover an interaction between neutrons and electrons was made by Dee in the same year, 1932 in which the neutron was discovered by Chadwick [7,8]. Discovery of the neutron by Chadwick in 1932 may be viewed as the birth of the strong interaction: it indicated that nucleus consists of protons and neutrons and hence the presence of force that holds them together, strong enough to counteract the electromagnetic repulsion. In 1936, Condon pointed out that the existence of a neutron - electron interaction would give rise to an isotope shift in spectral lines of atoms, which was observed for the first time by Aronberg in 1918 in the line spectra of Pb isotopes [9-11]. The existence of a weak attractive interaction between electrons and neutrons has been described in the series papers by Foldy [12].

Foldy has showed that neutron-electron interaction has two contributions - one arising from anomalous magnetic moment of the neutron and the other from an intrinsic Darwin coefficient-electric field. This picture was justifiable in meson theory though both of these contributions have a common origin [5,12,14]. In all methods of the measurements there are principal troubles connected with the necessity of introducing large corrections in size of order of the investigated effect of neutron - electron interaction [14].

Besides there is intrigue in the fact that all known experimental values were scattered around the so called Foldy scattering length in the interval 10%. The main conclusion of the fundamental papers by Foldy is that the intrinsic neutron-electron interaction is essentially an electromagnetic interaction between the neutron and the charge density producing an external electromagnetic field by electron [12,14-16].

According to contemporary physics the strong force does not act on lepton (electrons, positrons, muons and neutrinos), but only on protons and neutrons (more 3 generally, on baryons and mesons - this is the reason for the collective name hadrons). The strong interaction (also known as hadronic interaction) holds atomic nuclei together and, in another context, binds quarks within hadrons The baryons are bound states of three quarks, and mesons are composed of quark and antiquark [1,17].

It should be added that the forces between the quarks must be long range, because the gluons (as photons) have zero mass. This does not imply that the forces between hadrons are also long range, because hadrons have zero color charges overall. The forces between the colorless hadrons are the residues of the for as between their quark constituents, and cancel when the hadrons are far apart [1,16]. In 1935, Yukawa pointed out that the nuclear force could be generated by the exchange of a hypothetical spin less particle, provided its mass intermediate between the masses of proton and electron - a meson. Yukawa predicted the pion [1,17,18]. The macroscopic manifestations of the strong interaction are restricted up to now to radioactivity and the release of nuclear energy.

The Table 1 given for the strength and range of the forces come from a comparison of the effects they produce on two protons [19]. In some respect these resemble an ordinary Newtonian force between the protons, varying with the distance between them as if the force was derived from a potential function:

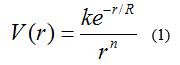
for some n. This is an inverse - power force which is diminished by an exponential factor at distances larger than a certain distance R, the range of the force. The strength of the force is measured by the constant k. The unit of strength is hc/2π where h is Planck’s constant and c the speed of light. Thus nuclear physics was essentially the paradigmatic example of understanding particle physics. The modern quantum mechanical view of the three fundamental forces (all except gravity) is that particles of matter (fermions neutrons, protons, electrons) do not directly interact with each other, but rather carry a charge, and exchange virtual particles (gauge bosons photons, gluons, gravitons) which are the interaction carriers or force mediators. As it can be seen from Table 1 [19], photons are the mediators of the interaction of electric charges (protons, electrons, positrons); and gluons are the mediators of the interaction of color charges (quarks). In our days, the accepted view is that all matter is made of quarks and leptons (Figure 1). As it can be seen, of the three pairs of quarks and leptons, one pair of each - the quark u and d and the leptons e and υe (electrons neutrino) - are necessary to make up the everyday world, and a world which contained only these would seem to be quite possible.

Table 1: The four fundamental forces.

Here FQ-Field Quant, RS-Relative Strength, TC-S-Typical Cross- Section, TTS-Typical time scale.

As we can see above the method of the scattering particles allows to determine only length of scattering as well as the size and depth (highest) of the neutron’s potential. In the present paper we attempt to measure the energy of the neutron-electron interaction via spectroscopic study of the optical characteristics of solids with isotope effect at low temperature. Therefore, it is purpose of our paper to advance a description of the manifestation of strong nuclear interaction in solids, using partly published and new non-accelerator experimental results. Our spectroscopic measurement of the low temperature optical characteristics of LiH_xD_1-x crystals is permitted to quantitative study of the dependence of strong coupling constant, α_s, on the proton - neutron distance in the deuteron nuclei. Another purpose of our communications is to draw the attention of physical society towards the expansion of the QED boundary via taking into account new experimental non - accelerates manifestation of the residual strong interaction in solids. Below we will briefly describe the results of the optical spectroscopy of isotope - mixed crystals. We should underline that these crystals are different by term of one neutron from each other (using LiD crystals instead of LiH ones). In this paper we shall present all the details of our experimental results which we omitted in the previous paper and in a series of international conference.

Experimental

The apparatus used in our experiments has been described in several previous publications [20-23]. For clarity, we should mention here that immersion home-made helium cryostat and two identical double - prism monochromators were used. One monochromator was used for the excitation and the other, which was placed at right – angle to the first for analyzing the luminescence and scattering of light. In our experiments we investigated two kinds of crystals (LiH and LiD) which are differing by a term of one neutron.

Lithium hydride and lithium deuteride are ionic insulating crystals with simple electronic structure, four electrons per unit cell, both fairly well – described structurally (neutron diffraction) and dynamically (second – order Raman spectroscopy) and through ab initio electronic structure simulation. Among other arguments, LiH and LiD are very interesting systems due to their extremely simple electronic and energy structure and to the large isotopic effects when the hydrogen ions are replaced by the deuterium ones. On the other hand, the light mass of the ions, specially H and D, makes that these solids have to be considered like quantum crystals, and consequently, described theoretically by quantum theory. In a solid one deals with a large number of interacting particles, and consequently the problem of calculating the electronic wave functions and energy levels is extremely complicated. It is necessary to introduce a number of simplifying assumptions. In the first place we shall assume that nuclei in the crystalline solid are at rest. In an actual crystal this is of course never the case, but the influence of nuclear motion on the behavior of electrons may be treated as a perturbation for the case in which they are assumed to be at rest. Even with above assumption, however, we are still with a many – electron problem which can be solved only be approximative methods. In the case of solids, the most important approximative method which has been applied extensively is the so – called one – electron approximation.

In this approximation the total wave function for the system is given by a combination of wave functions, each of which involves the coordinates of only one electron. In other words, the field seen by a given electron is assumed to be that of the fixed nuclei plus some average field produced by the charge distribution of all other electrons [23]. The difference between a good conductor and a good insulator is striking. The electrical resistivity of a pure metal may be as low as 10^-10 ohm-cm at a temperature of 1 K, apart from the possibility of superconductivity. The resistivity of good insulator may as high as 10^-22 ohm-cm. They understand the difference between insulators and conductors, we shall use the band–gap picture (Figure 2). The possibility of band gap is the most important property of solids. The single crystals of LiH and LiD were grown from the melt by the modified method of Bridgeman-Stockbarger [20,21]. The crystals were synthesized from ⁷Li metal and hydrogen of 99.7% purity and deuterium of 99.5% purity.

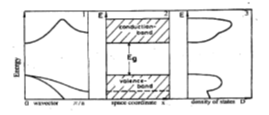
Figure 2: Various possibilities to present the band - structure of homogeneous undoped insulator (semiconductor). 1 - the dipersion relation, i.e. the energy E as afunction of the wave vector , 2 - the energy regions of allowed and forbidden statesas function of a space coordinate x and 3 - the density of states (all curves are schematic ones) [23].

Virgin crystals had a slightly blue - grey color, which can be attributed to nonstoichiometric excess of lithium present during the grown cycle. On annealing for several days (up to 20) at 500℃ under ~3 atm of hydrogen or deuterium, this color could be almost completely eliminated. Because of the high reactivity and high hygroscopy of investigated crystals should be protected against the surrounging atnosphere was necessing. Taking into account this circumstance, we have developed special equipment which is allowed to prepare samples with a clean surface cleaving their in the bath of helium cryostat with normal or superfluid liquid helium [20]. The samples with such surface allow to perform measurements during 15 hours.

An improved of LiH (LiD) as well as mixed crystals were used in the present study. In spite of the identical structure of all free – exciton luminescence spectra, it is necessary to note a rather big variation of the luminescence intensity of the crystals from the different batches observed in experiment (Figure 2). We should remind very briefly about the electronic excitations in solids. According to modern concept, the excitons can be considered [23] as the excited of the N – particles system: An electron from the valence band is excited into the conduction band (Figure 2). The attractive Coulomb potential between the missing electron in the valence band, which can be regarded as a positively charged hole, and the electron in the conduction band gives a hydrogen - like spectrum with an infinitive number of bound state and ionization continuum (Figure 3).

Below we will briefly describe the results of the optical spectroscopy of isotope - mixed solids. In our experiments we have investigated the low – temperature optical spectra (reflection, luminescence and scattering of light) of LiH_xD_1-x crystals (0≤x≤1) which are differ by term of one neutron from each other (Figure 3).

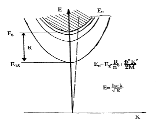
Figure 3: Discrete and continous (hatched area) Wannier - Mott exciton energy spectrum taking into account its kinetic energy h²k²/2M. The broken line connects to the dispersion of light in the medium. R - is the exciton binding energy, n=1, 2, 3, ....

Results

The usual way to determine the optical properties of a solid is to shine monochromatic light onto an appropriate sample and then to measure the reflectance or transmittance of the sample as a function of photon energy. In the spectral region of greatest interest is generally quite high, so that often a negligible small fraction of the incident light is

transmitted. It is the main reason, that the most experiments are measurements of the reflectivity. The mirror reflection spectra of mixed and pure LiH and LiD crystals, cleaved in superfluid helium are presented on Figure 4. All spectra have been measured with the same

apparatus under the same conditions. As can clearly see in Figure 4 all spectra exhibit a similar long – wave structure. As the deuterium concentration increases, the long – wave maximum (n _ 1S excitons [23]) broadens and shifts towards the shorter wavelengths. The energy values of exciton maxima for pure and mixed crystals at 2 K are presented in Table 4 of reference [25]. As demonstrated early most low - energy electron excitation in LiH crystals are the large - radius excitons [22,23] (Figure 4).

Figure 4: Mirror reflection spectra of indicated crystals at 2 K. Light source without crystals indicates by lamp.

Photoluminescence is the optical radiation emitted by a physical system (in excess of the thermal equilibrium blackbody radiation) resulting from excitation to a nonequilibrium state by irradiation with light. Photoluminescence is also rapidly evolving into major basic research tool comparable to absorption (reflection) measurements in importance. Two reasons for this stand out as significant. First is the sensitivity of the luminescence technique. It often happens that features which are just discernible in absorption will completely dominate the luminescence spectra. The converse is also sometimes true, making

luminescence and absorption (reflection) complementary techniques. Second is the simplicity of data collection. In last half- century the luminescence method has become one of the most common techniques for studying excitons in dielectrics and semiconductors.

While the structure of spectra of fundamental reflection (absorption) depends on the internal degrees of freedom of Wannier – Mott exciton, the structure and shape of the luminescence spectrum are determined primarily by its external degrees of freedom. The latter are associated with the translation motion of large – radius exciton as a whole, with the translation mass M=m_e + m_h , where m_e and m_h – effective masses of electron and hole, respectively.

Free exciton luminescence is observed when LiH (LiD) crystals are excited in the midst of the fundamental absorption. The spectrum of free exciton photoluminescence of LiH crystals cleaved in superfluid helium consists of a narrow (in the best crystals, its half - width is ΔE≤ 10 meV) phononless emission line and its broader phonon repetitions, which arise due to radiated annihilation of excitons with the production of one to five LO phonons (Figure 5).

Figure 5: Photoluminescence spectra of free excitons at 2 K in LiH and LiD crystals cleaved in superfluid helium.

The phononless emission line coincides in an almost resonant way with the reflection line of the exciton ground state which is indication of the direct electron transition X₁ - X₄ of the first Brillouin zone [26]. The lines of phonon replicas form an equidistant series biased toward lower energies from the resonance emission line of excitons. The energy difference between these lines in LiH crystals is about 140 meV, which is very close to the calculated energy of the LO phonon in the middle of the Brillouin zone and which was measured in (see, e.g. [22] and references quoted therein) [26].

The isotopic shift of the zero – phonon emission line of LiH crystals equals 103 meV. As we can see from Figure 5 the photoluminescence spectrum of LiD crystals is largely similar to the spectrum of intrinsic luminescence of LiH crystals. There are, however, some distinctions one is related. Firstly the zero - phonon emission line of free excitons in LiD crystals shifts to the short-wavelength side on 103 meV. These results directly show the violation of the strong conclusion that the strong force does not act on leptons [1,17]. The second difference concludes in less value of the LO phonon energy, which is equal to 104 meV. The simplest approximation, in which crystals of mixed isotopic composition are treated as crystals of identical atoms having the average isotopic mass, is referred to as VCA [23].

When light is excited by photons in a region of fundamental absorption in mixed LiH_xD_1-x crystals at low temperature, line luminescence is observed (Figure 6), like in the pure LiH and LiD crystals. As before [25], the luminescence spectrum of crystals cleaved in superfluid liquid helium consists of the relatively zero - phonon line and its wide LO replicas. or the sake of convenience, and without scarfing generality, Figure 6 shows the lines of two replicas. Usually up to five LO repetitions are observed in the luminescence spectrum as described in detail in [20]. In Figure 6 we see immediately that the structure of all three spectra is the same. The difference is in the distance between the observed lines, as well as in the energy at which the luminescence spectrum begins, and in the half - width of the lines.

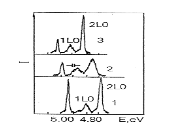
Figure 6: Photoluminiscence spectra of free excitons in LiH (1), LiH_xD_1-x (2) and LiD (3) crystals cleaved in superfluid helium at 2 K. Spectrometer resolution is shown.

At the excitation below the intrinsic absorption edge (E_n=1s=5.043 eV for LiD [22]) we have succeeded in observing the multiphonon RRS with the creation of up four phonons (Figure 7). Indeed, the energy difference between peaks in the RRS spectrum is equal the energy of the LO phonons in the center of the Brillouin zone [23,28].

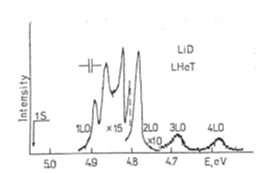
Figure 7: Resonant Raman scattering of a LiD crystals at the excitation E _ 4.992 eV at 4.2 K.

To pay attention the large half - width of observable lines in the RRS spectrum. As was shown in the paper their half - width are always larger than of the excitation line. The proximity of the exciting light frequency to the energy of exciton transitions leads to an essential modification of the selection rules for light scattering. The presence of the second - order  meV for LiH) in the RRS spectrum may be explained by a relatively strong scattering deformation mechanism in these crystals, where, however the main mechanism, as was seen from both figures, is Frőchlich mechanism of intraband scattering [23]. The long wavelength displacement of the excitation line frequency relatively exciton resonance a monotonic decrease the intensity of RRS spectrum as whole more than 60 - fold in both LiH and LiD crystals [22].

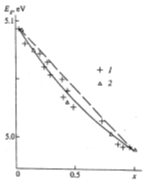
Figure 8: Dependence of the interband transition (strong interaction strength) energy E_g in mixed crystals on the concentration x (number of neutrons N). The straight dashed line is the linear dependence of coupling constant strong interaction α_s=f(N) [E_g= f(x) in the virtual model. The solid line corresponds to calculation using the polynom of second degree α_s= α_s=(LiD)+ [α_s(LiH- α_s(LiD)- b]x-bx² , where,      b=0. 046 eV is curvature parameter [23]. Points derived from the reflection spectra indicated by crosses and those from luminescence spectra by triangles.

Figure 8 shows the concentration dependence of the energy of interband transition E_g (Figure 2). As can be seen from Figure 8, VCA method (the straight dashed line) cannot describe observed experimental results. This dependence has a nonlinear character.

Comparison the experimental results on the luminescence (reflection) and light scattering in the crystals which differ by a term of one neutron only is allowed to the next conclusions;

1. At the adding one neutron (using LiD crystals instead LiH ones) is involved the increase exciton energy on 103 meV.

2. At the addition one neutron the energy of LO phonons is decreased on the 36 meV, that is direct seen from luminescence and scattering spectra.

Both characteristics are macroscopic.

Discussion

Traditionally nuclear - electron interaction (in our case neutron - electron interaction) taking into account the solving of Schrödinger equation using Born – Oppenheimer (adiabatic) approximation [29]. Since electrons are much faster and lighter than the nuclei by a factor nearly 2000 the electron charge can quickly rearrange itself in response to the slower motion of the nuclei, and this is the essence of the Born – Oppenheimer approximation. This approximation results the omission of certain small terms which result from the transformation. As was shown in [30] the eigenvalue (energy) of the electronic Schrödinger equation (equation 6 in [28]) depends on the nuclear charges through the Coulomb potential, but it doesn’t include any references to nuclear mass and it is the same for the different isotopes. The independent of the potential energy (the eigenvalue of the Schrödinger equation) is the essence adiabatic approximation. However, we must repeat, that the Born - Oppenheimer approximation is the standard anzatz to the description of the interaction between electrons and nuclei in solids [31].

The last result is forcing us to search for new models and mechanisms of nuclear - electron interaction including results of subatomic physics, e.g. hadron - lepton interaction. Out of four known interactions, three are described by SM - the electromagnetic, weak and strong ones. The first two of them have a common electroweak gauge interaction behind them. The symmetry of this interaction SU(2)_L X U(1)_Y manifests itself at energies higher than ~200 GeV. At lower energies, this symmetry is broken down to U(1)_EM≠U(1)_Y (the electroweak symmetry breaking): in SM this breaking is related to the vacuum expectation value of a scalar field [17]. The strong interaction in SM is described by the QCD, a theory with the gauge group SU(3)_C. The effective coupling constant of this theory grows when the energy decreased. As a result, particles which feel this interaction cannot exist as free states and appear only in the form of bound states called hadrons [1].

Most of modern methods of quantum field theory work at small values of coupling constant, αs, [32], that is, for QCD, at high energies. Quarks and leptons, the so - called SM matter fields, are described by fermionic fields. Quarks take part in strong interactions and compose observable bound state hadrons. Both quarks and leptons participate in the electroweak interaction. The matter fields constitute three generation: particles from different generation interact identically but have different masses [17]. For the case of neutrino, Yukawa interactions are forbidden as well, so neutrinos are strictly massless in SM (see, however [30] and references therein)).

The gauge bosons, which are carriers of interactions, are massless for unbroken gauge groups U(1)_EM (electromagnetism 13 - photons) and SU(3)_C (QCD - gluons), masses of W^± and Z₀ bosons are determined by the mechanism of electroweak symmetry breaking. It should be noted that the forces between the quarks must be long rang, because the gluons have zero mass. This does not imply that forces between hadrons are also long range, because hadrons have zero color charges overall. The forces between the colorless hadrons are the residues of the forces between their quark constituents, and cancel when the hadrons are far apart.

Returning to our non - accelerator experimental results, we should underline that in this paper we measure the strong nuclear interaction in crystals which differ by term of one neutron from each other. When we add one neutron in the hydrogen nucleus, we artificial activated of the strong interaction. As far as the gravitation, electromagnetic and weak interactions are the same in both kind crystals (LiH and LID), it only changes the strong interaction. Therefore a logical conclusion is made that the renormalization of the energy of electromagnetic excitations (isotopic shift equals 0.103 eV) is carried out by strong nuclear interaction.

The short range character of the strong interaction of nucleons does not possess direct mechanism of the elementary excitation (electrons, excitons, phonons) energy renormalization, which was observed in our low temperature experiments. Second reason that the interpretation of our experimental results is very difficult task because they are first demonstration of the violation of the strong conclusion in nuclear and particles physics that the strong nuclear force does not act on the colorless leptons [1,32]. Moreover we have some contradictions taking into account that the forces between quarks must be long range, because the gluons have zero mass. But as was mentioned above, the short range when forces between the colorless hadrons are the residues of the forces between their quark constituents, and cancel when the distance between hadrons is more than nuclear size [17].

We can see that the nuclear size transforms long range interaction in the short range strong one. It is very old question which up to present time has not any theoretical explanation. In spite of above discussion, at present time we can distinguish the following mechanisms of the isotopic shift zero phonon line:

1. Long range electric field of the neutron’s quarks. This mechanism owing to the confinement quarks is limited by the boundary of the neutron.

2. The possible new structure of the quarks and leptons - so - called preons [33].

3. The most likely mechanism of the neutron - lepton interaction is connected to the magnetic - like strong field of neutron’s quarks. Taking into account anomalous magnetic moment of the neuron [14,34] in the paper [5] was obtained the value of strong coupling

constant α_s=2.4680. Quite large value in comparison with the accelerator technique value _α_s(M_Z)=0.1198 [32]. The large value α_s is thus justified to think that residual strong forces acting beyond nucleon could exist. A possible interpretation is to assume that in addition to the 8 gluons predicted by QCD SU(3)_c group there is a ninth gluon color singlet [17].

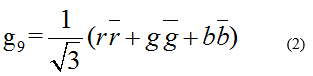
This massless photon - like gluon may be strongly interacts between nucleons (neutrons) and leptons (electrons) [1,17]. Returning to Figure 8 we can note that our measurements permit value to obtainment of strong coupling constant from _ α_s=2.4680 (pure LiD crystals) to α_s=0 (pure LiH crystals). Moreover, in Figure 9 we show the dependence of α_s on neutron’s number in different substances. We can see as early in the case of pure LiD crystals we have non - linear dependence of α_s on the neutron’s number in different substances, which as in the case LiH_xD_1-x doesn’t have any theoretical explanation (Figure 9). 

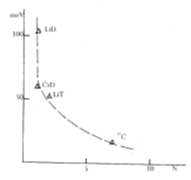
Figure 9: The dependence of the strong force on the number of neutrons in different substances.

Thus, the tentative interpretation of describing non-accelerator experimental results does not find consistent explanation at the change of strong interaction leaving to another mystery of SM [6]. We should remind that intrinsic contradiction of Standard Model is already well - known. Really, the Lagrangian of quantum chromodynamics (theory of the strong interaction) has the next form [19]:

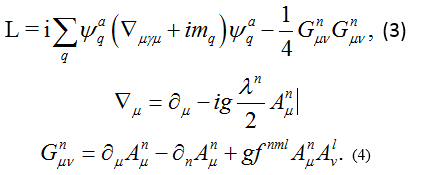
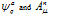quark and gluon fields, a_1,2,3,...8 are color indices λⁿ, and f^nml are Gell- Mann matrices and f symbols, m_q - are bare (current) masses, q=u, d, s, c, ... different quarks. It is common place [1,32] that the Lagrangian (3) contains the members which describe both free motion and interaction between quarks and gluons, which is defined by the strength couple g. Spacing of which it is necessary to remark that although the Lagrangian (3) possesses rather attractive peculiarities [19,30,33], its eigenstates are the quarks and the gluons which are not observed in free states [17,35-37]. The observed hadrons in the experiment don’t eigenstates in quantum chromodynamics. It is obvious to expect that the modern theory of QCD should finally overcome these difficulties, for example inserting QCD in QED.

Conclusion

The artificial activation of the strong nuclear interaction by adding one (two or more) neutrons in atomic nuclei leads it to the direct observation of the strong interaction in low - temperature optical spectra of solids. This conclusion opens new avenue in the investigation of the constant of strong nuclear interaction in the wide value range by means the condensed matter alike traditional methods. Our experimental non-accelerator results may shed light on a number of fundamental puzzles in modern physics, particularly on the unification of forces. Experimental observation of the renormalization of the elementary excitation energy of solids by the strong nuclear interaction stimulates its count in the process of description of the elementary excitations dynamics in quantum electrodynamics. Besides, we should highlight that such important information has been obtained via rather simple and inexpensive experimental physics equipment. Present article continuous to develop between nuclear, high energy and condensed matter physics.

References

1. Perkins DH. Introduction to High Energy Physics (2000)  CUP, Cambridge.
2. Sakharov AD. Vacuum quantum fluctuations in curved space and the theory of gravitation (1968) Sov Phys Dokl 12: 1040-1041.
3. Ling Jun Wang. Unification of gravitational and electromagnetic fields (2018) Physics Essays 31: 81-88. https://doi.org/10.4006/0836-1398-25.1.91
4. Barut AO. Unification based on electromagnetism (1986)  Annalen Phys (Leipzig) 498: 83-92.
5. Plekhanov VG and Buitrago JG. Evidence of residual strong interaction at nuclear - atomic level via isotopic shift in LiH - LiD crystals (2019) Prog Phys 15: 68-71.https://doi.org/10.18429/JACoW-IPAC2019-MORTS067
6. Cottingham WN, Greenwood DA. An Introduction to the Standard Model of Particle Physics (2007) CUP, Cambridge.
7. Dee PI. Attempts to detect the interaction of neutrons with electrons (1932) Proc Roy Soc (London) A136: 727-736. https://doi.org/10.1098/rspb.1932.2633
8. Chadwick J. The existence of a neutron (1932) Proc Roy Soc (London) A136: 692708. https://doi.org/10.1098/rspb.1932.2633
9. Aronberg. Note on the spectrum of the isotopes of lead (1918) Astrophys J 47: 96-101.
10. Striganov AP and Donzov Ju P. Isotope effect in atomic spectra (1955) Uspekhi Fiz. Nauk (Moscow) 55: 315-330 (in Russian).
11. King WH. Isotope shift in atomic spectra (1984) Plenum Press, New York.
12. Foldy LL. The electromagnetic properties of Dirac particles (1952) Phys Rev 87: 688-696. https://doi.org/10.1103/PhysicsPhysiqueFizika.1.i
13. Darwin CG. The wave equations of electron (1928) Proc Roy Soc (London) A118: 654- 680. https://doi.org/10.1098/rspb.1928.2633
14. Alexandrov Yu A. The fundamental properties of neutron (1982) Energoizdat, Moscow (in Russian).
15. Foldy LL. Neutron - electron interaction (1958) Rev Mod Phys 30: 471-481.  https://doi.org/10.1103/Rev.Mod.Phys.30.471
16. Mitsyna LV, Nikovenko VG, Parzhitski SS, et al., Extraction of the neutronelectron scattering length (2005) Eur Phys J C40: 473-482. https://doi.org/10.1051/epjap/2012110295
17. Griffiths G. Introduction to elementary particles (2008) Wiley - WCH, Weinheim.
18. Yutaka Y. On the interaction of elementary particles (1935) Proc Phys Math Soc 17: 48-57.
19. Henley EM and Garcia A. Subatomic physics (2007) World Scientific Publishing Co., Singapore.
20. Plekhanov VG. Macroscopic manifestation of the strong nuclear interaction in the optical spectra of solids (2018) In Proc 25 ISINN, Dubna, Russia.
21. Plekhanov VG. Isotope-induced energy-spectrum renormalization of the Wannier-Mott exciton in LiH crystals (1996) Phys Rev B54: 3869 - 3877. https://doi.org/10.1103/physrevb.54.3869  
22. Plekhanov VG. A possible signature of neutron quarks - leptons via gluon interaction in solids (2018) Proc 21th Int Conf Cond Matter Nucl Sci, Fort Collins, Colorado, USA.
23. Plekhanov VG. Giant isotope effect in solids (2004)  Stefan University Press, La Jola, CA.
24. Knox RS.  Theory of excitons (1963) Academic Press, New York, London.
25. Plekhanov VG. Isotopic and disorder effects in large exciton spectroscopy (1997) Phys Uspekhi 40: 553-568. https://doi.org/10.1016/0550-3213(71)90395-6
26. Baroni S, Pastori Parravicini G, Pezzica G. Quasip particle band structure of lithium hydride (1985) Phys Rev B32: 4077 - 4083. https://doi.org/10.1103/PhysRevB.32.4077
27. Verble JL, Warren JL and Yarnell JL. Lattice dynamics of lithium hydride (1968) Phys Rev 168: 980-989. https://doi.org/10.1103/PhysRev.168.980
28. Born M and Oppenheimer JR. On the quantum theory of molecules (2000) Quantum Chemistry, World Sci Publ Co., Singapore. https://doi.org/10.1142/9789812795762_0001
29. Plekhanov VG. Measurements of the wide value range of strong interaction coupling constant (2019) SSRG - IJAP 6: 32-37. https://doi.org/10.14445/23500301/IJAP-V6I3P106  
30. Martin RM. Electronic structure-basic theory and practical methods (2004) CUP, Cambridge.
31. Deur SJ, Brodsky GF, Teramond. The QCD running coupling (2016) Prog Part Nucl Phys 90: 1-74. https://doi.org/10.1016/j.ppnp.2005.07.003
32. Plekhanov VG. Modern view of the origin of isotope effect (2018) Lambert Academic Publishing, Saarbrücken, Germany.
33. Ioffe BL. The Origin mass and experiments on future high – energy accelerators (2006) Phys Uspekhi (Moscow) 49: 1077-1078.
34. https://doi.org/10.1070/PU2006v46n1ABEH000264
35. Kronfeld AS.  Lattice gauge theory and the origin of mass, in, one hundred Years of subatomic physics (2013) Henley E and Ellis S (Edtrs) World Sci Publ, Singapore.
36. Plekhanov VG. Necessity Additions (2019) Phys Uspekhi (Moscow) 61: 449-450. https://doi.org/10.3367/UFNe2019.07.038617
37. Dremin IM, Kaidalov AB. Quantum Chromodynamica and the phenomenology of strong interaction (2006) Phys Uspekhi (Moscow) 49: 263-273. https://doi.org/10.1070/PU2006v46n1ABEH000264

^*Corresponding author: 

Plekhanov VG, Fonoriton Scientific Laboratory, Garon Ltd., Tallinn, 11413, Estonia, E-mail: vgplekhanov@gmail.com    

Citation: 

Plekhanov VG. Isotope effect is the paradigm of a non-accelerator study of the residual nuclear strong interaction (2020) Edelweiss Chem Sci J 3: 8-14

Keywords

Strong interaction, Quarks, Gluons, Excitons, Phonons, Quantum chromodynamics and Electrodynamics