Explore journal overview, editorial leadership, indexing, articles in press, latest published work, and highlights from previous issues.
Research Article :
Emil Chibowski,
Aleksandra Szcześ and Lucyna Hołysz Magnetic
Field (MF) effects on water and dispersed systems have been studied for more
than half of century. However, so far there is no complete understanding of the
observed changes in the properties of studied systems if it is solely based on
the classical theories of magnetic field action. In Part I of this paper we
presented results of MF influence on the evaporation rate of aqueous solutions of
anionic surfactant Sodium Dodecyl Sulphate (SDS) and cationic one Dodecyl
Trimethylammonium Bromide (DoTAB). In this paper static magnetic field effects
on the surface tension of the above-mentioned surfactants are presented. The
concentrations of the solutions used were both below and above their Critical
Micelle Concentration (CMC). The solutions were under the MF action for 60 min
in a closed vessel and were stirred by hand every 15 min. Previously it was
found that the surface tension of pure water (distilled in a quartz apparatus)
decreased by 2.1 mN/m after similar the MF treatment. Moreover, the memory
effect lasted longer than 60 min. In case of the surfactant solutions the surface
tension changed depending both on the kind of surfactant and its concentration.
Bigger changes were observed for cationic DoTAB. In the solutions below their
CMC the surface tension was lower after MF treatment. However, the surface
tension of DoTAB solution at CMC increased several mN/m after the MF treatment.
In the solutions concentrated above the CMC, respectively, the MF effects were
practically vanishing. The observed changes are discussed in detail considering
the structure of the surfactant adsorbed layers and acceleration force acting
on the ions which was calculated from the Lorentz equation. To our knowledge,
such results are published in the literature for the first time and they should
be considered as preliminary ones. More systematic experiments are needed to
better understand the observed changes. Introduction Magnetic Field (MF) effects observed
during and after its action on water and aqueous solutions are still
interesting but debatable issues despite they have been studied for over 50
years. Often the changes due to MF action were considered as those resulting in
the hydrogen bonding changes both in the water intra-clusters and
inter-clusters [1-4] but the most remarkable progress was achieved in 2012 by
Coey [5] who to explain the magnetic field action applied the non-classical
theory of nucleation mechanism to the formation of Dynamically Ordered Liquid
Like Oxyanion Polymers (DOLLOP) [6,7]. Moreover, it was also shown that to
obtain any MF effect the gradient of the field is more important than the field
strength itself [8,9]. A review of latest approaches to the MF understanding
was published lately [10]. Many papers have been published in which the MF
effects observed in pure water at different conditions are reported. Often the
changes in evaporation rate and surface tension were investigated [11-20].
Surprisingly, despite the fact that a huge number of papers on the MF effects
have been published, we could not find any paper reporting results about the MF
effects on surfactant solutions. On the other hand, many different surfactants
are present in the environment, e.g. in surface and waste waters, soil, many
industrial waters, sewage treatment plants, laundry, etc. [21,22]. Therefore,
it seemed interesting to
learn whether any MF effects will appear after a surfactant solution treatment
with the magnetic field. In
the previous paper evaporation rate of water from 10-3 M anionic surfactant Sodium Dodecyl Sulphate (SDS) and
cationic Dodecyl
Trimethylammonium Bromide (DoTAB) surfactants solutions were studied [23].
The evaporation rate of water from both surfactants solution increased in the
MF presence, similarly like it was found for pure water [20]. However, in the
absence of MF water evaporated slower from SDS solution than from pure water
while from DoTAB on the contrary. These differences were explained taking into
account drastic differences in the ionic groups properties and size. The SDS
head group -SO3-Na+ can form three strong
hydrogen bonds with water molecules while the DoTAB head group -N+(CH3)3Br-
only one weak hydrogen bond can appear, if ever. Moreover, this group shows
hydrophobic properties due to the presence of three methyl -CH3
groups and it is more than 3 times larger than the sulfate. All these
differences are the reasons of different respond of the two surfactant
solutions to the MF action. Having
known MF effects on the evaporation rate of anionic and cationic surfactant
solutions it became interesting to study the MF effect on the solutions surface
tension, which is most characteristic parameter for such solutions. Moreover,
lowering of water surface tension is of principal importance of practical
applications of surfactants. However, so far MF effects on the surface tension
of a surfactant have not been investigated despite the fact that the results
would have practical applications. Experimental Static magnetic field (max. 0.65T)
originating from three connected ring Nd magnets (MP 86 x 58 x 35 mm each) was
applied. The sample of anionic Sodium Dodecyl Sulfate (SDS) or cationic Dodecyl
Trimethylamonium Bromide (DoTAB) solutions was placed in the magnet for 60 min
in a closed plastic vessel. All the experiments were carried out at room
temperature and humidity. Every 15 min the vessel was stirred manually for a
while. The investigated concentrations of the surfactants solution were below
or above their CMC, respectively. The solutions were prepared using Milli-Q
water. Figure 1 shows the
magnets and the MF strengths, and the vessel with the samples inside the
magnet. The changes in the MF field strength at the edge of the ring and at its
center with the distance from the magnet were published in the previous paper
[20,23]. First some preliminary tests have been carried out to learn how the MF
treatment time of the solutions affects the surface tension. For this purpose
the 10-3 M SDS and DoTAB solutions were MF treated for 15 min and 30
min and 60 min. After each 15 min of the MF treatment the sample was stirred by
hand for a while. The surface tension was measured using the automatic KSV
Sigma 700 ring tensiometer. Simultaneously
surface tension of given MF-untreated surfactant solution was measured. At
least five to ten measurements of each sample were taken automatically and the
mean value and standard deviation were recorded. Results
and Discussion The
results presented in Figure 2 show
how the time-span of the MF treatment influences the surface tension of the
solutions. In the case of SDS solution an increasing effect is observed with
increasing treatment time but in the case of DoTAB such dependence is not
straight. However, it needs further systematic investigations which will be the
subject of a paper to follow. For present studies the 60 min MF treatment time
have been selected. The
mean results of the subsequent measurements of surface tension of MF treated
and untreated SDS solution samples are presented in Figure 3 for 0.001 M, 0.005 M and 0.01 M solutions. The surface
tension of the magnetically treated solutions was measured immediately after
the solution taking off the magnet. It usually took 3-5 min. As can be seen MF
decreases surface tension of the solutions by 5.69 mN/m, 1.54 mN/m and 0.51 mN/m,
respectively. It is clearly seen that with increasing the SDS solution
concentration MF effect is smaller. It should be also stressed that the 0.01M
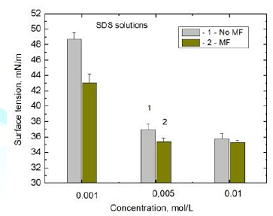
concentration is a little larger than the CMC of SDS which amounts 0.0082 M. The
results of MF effects on DoTAB solution surface tension
are shown in Figure 4. Comparing the
results with those of Figure 3 the MF effect on the surface tension of this
surfactant is much larger than that on SDS solutions. The surface tension of
0.001 M DoTAB solution decreased by 11.48 mN/m while the surface tension of
0.001 M SDS has decreased by 5.69 mN/m only. Similarly, in the case of 0.005M
solutions the decrease in the surface tension is 5.72 mN/m and 1.54 mN/m,
respectively. Moreover, the surface tension of 0.01M DaTAB solution after MF
treatment increased by 5.95 mN/m and that of 0.05 M decreased by 0.85 ± 0.07
mN/m only. The 0.01M concentration is very close to CMC of DoTAB (0.011M) and
0.05M is significantly larger than CMC. The same values of surface tension of
the untreated DoTAB solutions were reported by Acosta et al. [24]. To better
depict the MF effects on the surface tension of these two surfactants solutions
in Figure 5 are shown the surface
tension changes for all investigated concentrations. As it can be seen if the
concentration is lower than the respective CMC, the surface tension of both
surfactants is lowered by the MF action and a greater surface tension decrease
is observed for cationic DoTAB than anionic SDS solutions. However, an increase
in the surface tension (5.9 mN/m) of this surfactant solution occurs if the
concentration (0.01M) is practically equal to its CMC (0.0011 M). If the
concentrations of both surfactants are greater than their CMC the MF effects
are very small, where the changes of surface tension are less than 1 mN/m
(Figures 3-5). The
above results were elaborated statistically using the two-tailed t-Student test
at 5% significance level. The results are collected in Table 1 where it can be seen that all the differences between MF
treated and untreated solutions of the surfactants are statistically
significant (p<<α). The mean values of the surface tension for each
concentration were calculated from 5-8 individual experiments in which 10-15
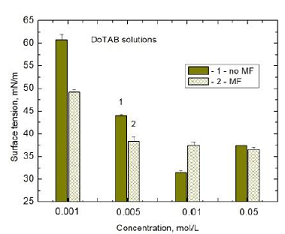
times the surface tension was measured using the ring method. Figure 4:
Mean surface tension values of DoTAB 0.001M, 0.005 M, 0.01 M, and 0.05 M
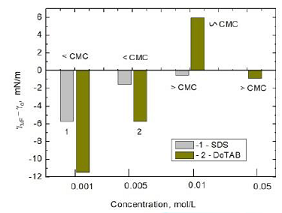
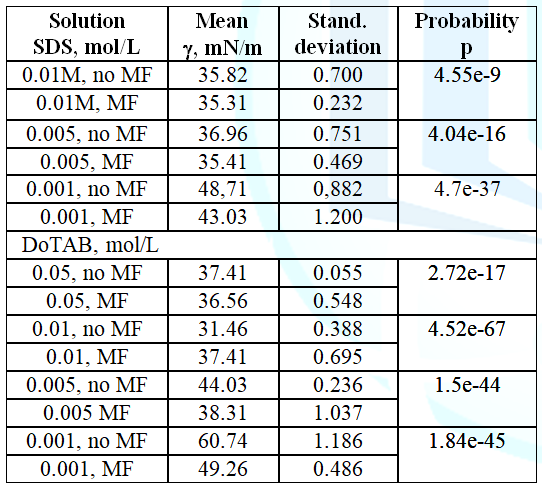
solutions: 1-MF-untreated and 2-60 min MF-treated samples. Table 1: Results of the
two-tailed t-Student test for untreated and MF treated SDS and DoTAB solutions
(significance level, α = 0.05). First
of all the size of the groups is different, which is 0.17 nm2 for
the SDS and 0.54 nm2 for the hard-core area of DoTAB. These values
were established from the bond lengths, bond angles, and atomic volumes via a
molecular model of the headgroup [25]. Also the distance from the hydrophobic
core surface to the centre of counterion location is 0.545 nm and 0.345 nm,
respectively [25]. Thus, the Na+ counterions are located at a larger
distance from the C12-O-SO3- headgroup than
Br- from the C12-N+(CH3)3. Moreover,
the SDS molecules oxygen atoms can form hydrogen bonds with water molecules,
which are not the case for DoTAB whose head is more hydrophobic because of
presence of three methyl -CH3
groups
and only a weak N…H
hydrogen bond can be formed [26]. Because -N+(CH3)3
group is over 3 times larger than the sulfate, therefore it can be expected
that less DoTAB groups (molecules) than those of SDS occupy the same surface
area of the solution. Moreover, the Br- counterions are located
closer to the heads [25], hence at the solution surface the interactions
between water molecule and head group of DoTAB is much weaker than in the case
of SDS. Generally,
the decrease in surface tension can be interpreted as due to an increase in the
surface concentration of surfactant. This conclusion results from the Gibbs adsorption equation relating the
surface excess amount of a surfactant with its bulk concentration and surface
tension. For
Equation 1 refer PDF From
Equation 1 results that if a surfactant surface tension decreases with
increasing its bulk concentration then the surface excess amount increases, but
only below the CMC when in the surface adsorption layer maximum adsorption and
packing of the molecules is not achieved yet. Assuming this interpretation, it
would mean that the MF effect relies on the increasing excess of SDS or DoTAB
molecules in the surface layer. Abandoning at this moment possible mechanism of
the MF force action, the increase in surface excess concentration can be easily
understood if the solution concentration is lower than CMC of SDS or DoTAB,
respectively (Figures 3-5). Actually, also the small decrease in surface
tension of the solution whose concentration is greater than CMC can be considered
as due to some small changes in the density and structure of the adsorbed
surface layer. Thus, in the case of 0.01 M SDS, this concentration is only
slightly larger than the CMC by 0.0018 M (0.01 M-0.0082 M). Therefore there can
be still some room in the surface layer for a closer SDS molecules packing
caused by MF force and hence the observed small decrease in the surface
tension. In the case of DoTAB after 60 min MF treatment the surface tension of
0.05 M decreases by 0.85 mN/m only. However, this small difference appeared to
be statistical significant (Table 1). On the other hand the surface activity of
surfactants can be described by Sprow and Prausnitz equation [27]. For
Equation 2 refer PDF Analogical
equation can be written for water molecules in the surface layer. For
Equation 3 refer PDF In
Equations 2 and 3 activity a of the
components are defined in the symmetrical system, i.e. aw, as
®1 if xw,
xs ®1, respectively. Zdziennicka et al. [28]
using Eq.3 and assuming that in diluted surfactant solutions its activity in
the bulk phase is small and hence that of water is close to unity calculated
activity of water in the surface layer from Eq.4 which results from Eq.3 if it
is assumed that awB ®1. For
Equation 4 refer PDF Where
meaning of the symbols are the same as that in Equations 2 and 3. In
the calculations they [28] used for water gw = 72.8 mN/m at 293K and the molar
surface area for water equal to 0.6023‧105 m2/mol. Then,
because For
Equation 5 refer PDF For
Equation 6 refer PDF In
the concentration range C below CMC of given surfactant (i.e. the range where
the surface tension of the solution gLV
vs.
C decreases linearly) the calculated from Equation 6 gs
values
appeared to be constant (31.8 ± 0.3 mN/m) for the all 11 studied surfactants,
among others SDS, CTAB and dodecyl dimethylethyl ammonium
bromide
[28]. Hence they concluded that the maximum reduction of water surface tension
equals to 72.8-31.8 = 41.0 mN/m. The value of gs= 31.8 mN/m lies
between the surface free energy of polyethylene crystallized in air (36 mJ/m2)
[30] and the surface tension of liquid hexadecane (27.5 mN/m). Generally, the
surface free energy of solid hydrocarbons is much higher if the hydrocarbon
chains are parallel than normal to surface. This is because of a lower surface
concentration of -CH3 than -CH2- groups, i.e. 0.19-0.25
nm2 and 0.05-0.057 nm2, respectively [30]. However, -CH3
interaction is 82% higher than -CH2- [31]. In the above calculation
the authors [28] assumed the cross-sectional area for water molecule equal to
0.1 nm2. Such value was determined for adsorbed water molecules
[31]. The van der Waals diameter (an imaginary hard sphere representing the
distance of closest approach) of water molecule is much smaller 0.282-0.32 nm
and therefore its cross-sectional area is 0.62-0.80 nm2 [32]. It
means that the surface area per water molecule in the surface layer can be
squeezed. The above mentioned maximum possible reduction of the surface tension
of water (41.0 mN/m) is smaller than the surface tension values of our MF
treated 10-3 M SDS and DoTAB solutions. However, if the
concentration of SDS is higher than 10-3 M the surface tension of
both MF treated and an untreated solution is 5-6 mN/m smaller than 41.0 mN/m
(Figure 3, Table 1). But such concentration is already behind the linear change
of surface tension versus concentration. The same is true for DoTAB solutions
but for 0.01 M and 0.05 M solutions (Figure 4, Table 1). The calculated from
Equation 6 values of gs for 10-3 M SDS amount
to 18.8 mN/m and 16.3 mN/m for untreated and MF treated solutions,
respectively, and the values for 0.001 M DoTAB solution equal to 25.4 mN/m and
17.4 mN/m, respectively. Thus calculated gs
values
for given solution can be interpreted as free energy of the surface layer built
up solely of the surfactant molecules. The layer structure and the molecules
orientation determine its free energy and changes similarly as that of the
n-alkanes series from n-pentane to n-hexadecane whose surface tension changes
from 15.8 mN/m to 27.5 mN/m, respectively. As
discussed above, bigger decrease in the surface tension of cationic than
anionic surfactant solutions caused by MF is probably due to the presence of
three -CH3 groups present in the DoTAB head group. The interaction
potential of this group is greater than –CH2– although the
surface density of the groups is lowers [30]. Hence the decrease in surface
tension of MF treated solutions may result from some reorientation of the
adsorbed surfactant molecules and changes in the surface layer structure. The
different properties of -N+(CH3)3 and -O-SO3-
groups reflected also in water rate evaporation from these surfactant
solutions. The former caused easier evaporation of water while the later
hindered it [23]. Additionally, the increased water evaporation from MF treated
DoTAB solution might be also due to weakening of Van der Waals interactions and
hydrogen bonds of the intra-clusters [2,33]. On the other hand, formation of
hydrogen bonds of water molecules with the oxygen atoms from -OSO3-
groups hinders water evaporation [23]. Van Oss and Constanzo [34] reported for
SDS immersed in water 23.8 mN/m for the surface tension of tails and 46 mN/m
for the electron-donor parameter Trying
to understand the observed magnetic field effects on the surface tension
changes of ionic surfactant solutions the Lorentz force action can be
considered. For
Equation 7 refer PDF The
first term represents the electric force acting on a moving charge v and
the second term expresses the magnetic force whose direction is perpendicular
to both the velocity of the charge and the magnetic field. The magnetic force
action depends on the charge q and the magnitude of so called
cross product of v × B, i.e. the velocity
and flux density vectors where the relative directions of these two vectors are
taken into account. Depending on the angle ϕ between v and B,
the magnitude of the force equals qvB
sin ϕ. If the angle ϕ = 90o, i.e. v is perpendicular to B,
the particle trajectory is circular with a radius of r = mv/qB. If the angle ϕ
is less than 90°, the particle will move along a helix having the axis parallel
to the field lines. Finally, if ϕ = 0o there will be no magnetic
force acting on the particle and it will continue moving along the field lines.
In an electrolyte solution the electric field density E is zero and only magnetic force of Equation 7 acts. Among others
Silva et al. [35] considered the Lorentz force to be
responsible for the observed MF effects which influenced the ion polarization,
especially bivalent cations which are hydrated more strongly than the anions. The
ions remained orientated up to two days (the memory effect) at the gas nanobubbles
dispersed in the solution. In consequence the precipitating particles of
calcium carbonate were smaller than those from the untreated solutions. Also
some changes in their crystalline structure were observed [35]. Taking
magnitude of the parameters as: v @ 0.992
m/s (evaluated experimentally), q =
3.2 ‧10-19 C (divalent cation), E = 0 (electrolyte solution) and B =
1T, the Lorentz force amounted to 3.17‧10-19 N. Because the ion mass
is 10-25-10-26 kg, therefore the acceleration (F/m) can
be as large as 106-107 m/s2, and it would
cause the ion polarization. Moreover, this was confirmed by experiments
conducted under the quiescent conditions where no changes in the liquid
viscosity or particles settling rates were observed [35]. In
our experiments the MF in the ring magnet changes radially from the top inner
edge to its center from 0.347 T to 0.053 T which occurs on the distance of 19
mm (Figure 1). The MF derivative ¶B/¶x on the surfactant sample surface
level equals to 43.18 T/m and 7.91 T/m, respectively. Hence MF gradient changes
from 14.96 T2/m to 0.42 T2/m, respectively (Figures 8 and
9 [20]). Assuming that during the samples stirring every 15 min the surfactant
ions in the solution move ca. 0.5 m/s and some of the ions cross
perpendicularly the field lines. Then the Lorentz force F = qvB for monovalent ion amounts to
(1.6×10-19 C × 0.5 m/s × 0.347 T) = 0.278×10-19 N. Hence the
acceleration force F/m imposed on the dodecylsufate ion C12-O-SO3-(4.406×10-25
kg/ion) amounts to 6.3 × 104 m/s2 while that acting
on C12-N(CH3)3+ (3.79 ×10-25
kg/ion) amounts to 7.3 × 104 m/s2. The force at the
magnet center is ca. 6.5 times lower than that at the edge. Although calculated
here acceleration force values are much lower than those calculated by Silva et
al [35] in the 1T magnetic field, it seems that they are still can influence
the surfactant surface monolayer formation and structure, which appears in the
observed changes of the solutions surface tension. Moreover,
the observed MF effects can be also considered as a result of the local
increase in the thermodynamic
potential.
Such approach was described in detail in the papers published by Cefalas et al.
[8,9] who explained why even in a weak external magnetic field (0.05 T)
aragonite precipitates instead of calcite, nevertheless that the later has
lower ground electronic state by 28 eV. They explained this phenomenon on the
basis of a macroscopic
antisymmetric coherent state. Such state can be induced by an external MF acting
on an ensemble of water two level molecular rotors (the water coherent state).
In the case of a conductive liquid, even in absence of a static MF, during the
flow there are present electromagnetic fluctuations and spontaneous magnetic
field. Quantum mechanics predicts that external magnetic field can amplify
magnetic fluctuations in the bulk liquid by exchanging the energy through an
angular momentum of water molecular rotors, as well as by such momentum of the
macroscopic turbulent flow. Thus, the energy transfer occurs via the angular
momenta of water molecules, the flow and the magnetic field. From the theoretical
calculation results that the received energy increases if the MF is in
resonance with the rotational frequencies of molecular rotors and low
frequencies of the turbulent flow [8]. Moreover, according to these authors
[8,9] such amplified state will last for a longer time because of “the
forbidden nature of transition between the anti-symmetric and the symmetric
state” [9]. This explains precipitation of CaCO3 as aragonite and
also so called memory effect in water which was many times reported in the
papers. Later Coey [5] proposed a theory explaining the MF effects which
considered the field gradient as more important than the MF strength itself. It
is based on a non-classical nucleation mechanism which takes into account the
presence of stable pre-nucleation clusters in calcium carbonate solutions. Next
this theory has been successfully verified by Sammer et al. [7]. Relating
these approaches to the observed changes in the surface tension of the
surfactant solutions it can be easier understood the surface tension changes as
due to the MF energy gained by the surfactant ions, the state of which lasts
sufficiently long to measure the changes after several minutes the MF had
ceased. It should be also mentioned that in the previously published paper [20]
we had observed decrease in the surface tension of pure water by 2.1 mN/m after
60 min of the same MF treatment. Moreover, after 60 min since the field removal
the surface tension was still by 1 mN/m smaller than that of the untreated
sample. Conclusions Static
Magnetic Field (MF) affects surface tension of anionic and cationic surfactant
solutions. A bigger effect has been found for cationic than anionic surfactant
solutions. The MF effects are very small in the solutions whose concentration
is higher than CMC of the given surfactant. The MF effects can result both from
the Lorentz force and the local increase in the thermodynamic potential. It can
be induced by an external MF acting on an ensemble of water two level molecular
rotors and can be explained on the basis of a macroscopic antisymmetric coherent state. The local
increase in the MF gradient can cause the effects too. The
presented results are somewhat preliminary and the above calculations and
hypotheses have to be verified by systematic studies. So far no MF effects
dealing with the surfactant solutions were published and there is no data for
any comparison. Therefore more experiments are needed to better understand the
observed changes and the above presented results should be treated as
preliminary ones.
This work was
supported by National Centre of Science, grant 2016/21/B/ST4/00987, which is
greatly appreciated. We are grateful to Ms. Weronika Głąb for the surface
tension measurements and MSc Michał Chodowski for statistical calculations. 1.
Toledo
EJL, Ramalho TC and Magriotis ZM. Influence of magnetic field on
physical-chemical properties of the liquid water: Insights from experimental and
theoretical models (2008) J Molecular Sci 888: 409-415. https://doi.org/10.1016/j.molstruc.2008.01.010 2.
Zhou
KX, Guiwu L, Zhou QC and Song JH. Monte Carlo simulation of liquid water in a
magnetic field (2000) J Appl Phys 88: 1802-1805. https://doi.org/10.1063/1.1305324 3.
Chang
KT and Weng CI. The effect of an external magnetic field on the structure of
liquid water using molecular dynamic simulation (2006) J Appl Phys 100: 043917.
https://doi.org/10.1063/1.2335971 4.
Cai
RH, Yang JH and ZhuW. The effects of magnetic fields on water molecular
hydrogen bonds (2009) J Mol Struct 938: 15-19. https://doi.org/10.1016/j.molstruc.2009.08.037 5.
Coey
JMD. Magnetic water treatment-how might it work? (2012) Philos Mag 92: 3857-3865.
https://doi.org/10.1080/14786435.2012.685968 6.
Demichelis
R, Raiteri P, Gale JD, Quigley D and Gebauer D. Stable prenucleation mineral
clusters are liquid-like ionic polymers (2011) Nat Comm 2: 590-598. http://doi.org/10.1038/ncomms1604 7.
Sammer
M, Kamp C, Paulitsch-Fuchs AH, Wexler AD, Cees J N, et al. Strong gradients in
weak magnetic fields induce DOLLOP formation in tap water (2016)Water 8: 79.
https://doi.org/10.3390/w8030079 8.
Cefalas
AC, Kobe S, Dražic G, Sarantopoulou E, Kollia Z, et al. Nanocrystallization of
CaCO3 at solid/liquid interfaces in magnetic field: a quantum approach (2008)
Appl Surf Sci 254: 6715-6724. https://doi.org/10.1016/j.apsusc.2008.04.056 9.
Cefalas
AC, Sarantopoulou E, Kollia Z, Riziotis C, Dražic G, et al. Magnetic field
trapping in coherent antisymmetric states of liquid water molecular rotors
(2010) J Comput Theor Nanosci 7: 1800-1805. https://doi.org/10.1166/jctn.2010.1544 10.
Chibowski
E and Szcześ A. Magnetic water treatment - A review of the latest approaches
(2018), Chemosphere 203: 54-67. https://doi.org/10.1016/j.chemosphere.2018.03.160 11.
Nakagawa
J, Hirota N, Kitazawa K and Shoda M. Magnetic field enhancement of water
vaporization (1999) J Appl Phys 86: 2923-2925. https://doi.org/10.1063/1.371144 12.
Kitazawa
K, Ikezoe Y, Uetake H and Hirota N. Magnetic field effects on water, air and powders
(2001) Physica B 294-295: 709-714. https://doi.org/10.1016/S0921-4526(00)00749-3 13.
Holysz
L, Szczes A and Chibowski E. Effects of a static magnetic field on water and
electrolyte solutions (2007) J Colloid Interface Sci 316: 996-1002. https://doi.org/10.1016/j.jcis.2007.08.026 14.
Szcześ
A, Chibowski E, Holysz L and Rafalski P. Effects of static magnetic field on
water at kinetic condition (2011) Chem Eng Process 5: 124-127. https://doi.org/10.1016/j.cep.2010.12.005 15.
Rashid
FL, Hassan NM, Jafar AM and Hashim A. Increasing water evaporation rate by
magnetic field (2013) Int Sci Invest J 2: 61-68. 16.
Guo
Y-Z, Yin D-C, Cao H-L, Shi J-Y, Zhang C-Y et al. Evaporation rate of water as a
function of a magnetic field and field gradient (2012) Int J Mol Sci 13: 16916-16928.
https://dx.doi.org/10.3390%2Fijms131216916 17.
Seyfi
A, Afzalzadeha R and Hajnorouzi A. Increase in water evaporation rate with
increase in static magnetic field perpendicular to water-air interface (2017)
Chem Eng Process 120: 195-200. https://doi.org/10.1016/j.cep.2017.06.009 18.
Amor
HB, Elaoud A, Salah NB and Elmoueddeb K. Effect of Magnetic Treatment on
Surface Tension and Water Evaporation (2017) Intern J Advan Ind Engin 5:
119-124. http://dx.doi.org/10.14741/Ijae/5.3.4 19.
Mang
Y, Wei H and Li Z. Effect of magnetic field on physical properties of water
(2018) Results Phys 8: 262-267. https://doi.org/10.1016/j.rinp.2017.12.022 20.
Chibowski
E, Szcześ A and Hołysz L. Influence of magnetic field on evaporation rate and
surface tension of water (2018) Colloids Interfaces 2: 68. https://doi.org/10.3390/colloids2040068 21.
Ivanković
T and Hrenović J. Surfactants in the environment (2010) J Surfactants
Environment 61: 95-110. https://doi.org/10.2478/10004-1254-61-2010-1943 22.
Olkowska
E, Polkowska Z and Namiesnik J. Analytics of surfactants in the environment:
problems and challenges (2011) Chem Rev 111: 5667-5700. https://doi.org/10.1021/cr100107g 23.
Chibowski
E and Szcześ A. Magnetic field effects on aqueous anionic and cationic
surfactant solutions. Part I: Water evaporation, submitted for publication. 24.
Acosta
EJ, Mesbah A and Tsui T. Surface activity of mixtures of dodecyltrimethyl
ammonium bromide with sodium perfluorooctanoate and sodium octanoate (2006) J
Surfactants Detergents 9: 367-376. https://doi.org/10.1007/s11743-006-5015-y 25.
Fujiwara
F, Reeves LW, Suzuki M and Vanin JA. Studies of lyotropic liquid crystals that
align in magnetic fields (1979) In: Proceedings of Colloids and Surface Science
Symposium, University of Tennessee, Solution chemistry of surfactants, USA 1:
63-78. 26.
Nagarajan
R and Wang C-C. Theory of surfactant aggregation in water/ethylene glycol mixed
solvents (2000) Langmuir 16: 5242-5251. https://doi.org/10.1021/la9910780 27.
Sprow
FB and Prausnitz JM. Surface thermodynamics of liquid mixtures (1992) Can J ChemEng
6: 25-28. https://doi.org/10.1002/cjce.5450450106 28.
Zdziennicka
A, Szymczyk K, Krawczyk J and Jańczuk B. Activity and thermodynamic parameters
of some surfactants adsorption at the water-air interface (2012) Fluid Phase
Equilibria 318: 25-33. https://doi.org/10.1016/j.fluid.2012.01.014 29.
Chattoraj
DK, Halder E, Das KP and Mitra A. Surface activity coefficients of spread
monolayers of behenic acid salts at air–water interface (2006) Adv Colloid
Interface Sci 123-126: 151-161. https://doi.org/10.1016/j.cis.2006.05.002 30.
Fowkes
FM. Calculation of work of adhesion by pair potential summation (Ed) Fowkes FM (1969)
Acad Press, UK, 151-163. https://doi.org/10.1016/B978-0-12-395594-4.50021-X 31.
Van
Olphen H. Determination of surface areas of clays- evaluation of methods (Eds)
Everett DH and Ottewill RH (1970) Surface Area Determination: Proceedings of
the International Symposium on Surface Area Determination Held at University of
Bristol, UK 255-272. https://doi.org/10.1016/B978-0-408-70077-1.50027-0 32.
Chaplin
M. Water Structure and Science 33. Krems RV.
Breaking van der Waals molecules with magnetic fields (2004) Phys Rev Lett 93: 013201.
https://doi.org/10.1103/PhysRevLett.93.013201 34.
Van
Oss CJ and Costanzo PM. Adhesion of anionic surfactants to polymer surfaces and
low energy materials (1992) J Adhesion Sci Technol 6: 477-487. https://doi.org/10.1163/156856192X00809 35.
Silva
B, Queiroz Neto JC and Petria DFS. The effect of magnetic field on ion
hydration and sulfate scale formation (2015) Colloid Surf A 465: 175-183.
https://doi.org/10.1016/j.colsurfa.2014.10.054 Emil
Chibowski, Professor, Department of Physical Chemistry-Interfacial Phenomena,
Faculty of Chemistry, Maria Curie-Skłodowska University, 20-031 Lublin, Poland,
E-mail: emil.chibowski@umcs.pl
Chibowski
E, Szcześ A and Hołysz L. Magnetic field effects on aqueous anionic and cationic
surfactant solutions part II: surface tension (2019) Edelweiss Chem Sci J 2: 1-6 Magnetic field effects, Anionic and cationic
surfactant, Surface tension changesMagnetic Field Effects on Aqueous Anionic and Cationic Surfactant Solutions Part II: Surface Tension
Abstract
Full-Text
Both
surfactants possess the same chain-lenth containing 12 carbon atoms. However,
their polar (ionic) heads are completely different, i.e. -OSO3–H+
and -N+(CH3)3Br-:
+ 
= 1 and the adsorbed film pressure π is
expressed as [29]:of -SO4 head, which is
responsible for the hydrogen bonds formation. From the surface tension values
of SDS solutions (Figure 3 and Figure 4) results that the principally determines the surface
tension. As for the increase in surface tension of MF treated 10-2 M
DoTAB solution (Figure 3 and Figure 4), which is very close to the CMC but a
little below, it can be interpreted as the restructuring of the almost fully
packed surface layer. From the Gibbs adsorption equation (Equation 1) it can be
concluded that MF enhances formation of micelles in the bulk solution and hence
reduces the effective DoTAB bulk activity which appears in a small increase of
the solution surface tension. However, the observed decrease in the DoTAB
surface tension of the solutions in the rest cases leads to the conclusion that
MF increases amount of the adsorbed surfactant molecules in the surface layer
and/or causes the layer restructuration (the molecules reorientation) if below
CMC and practically has no effect on the solutions at a higher concentration
than CMC.Acknowledgements
References
*Corresponding author
Citation
Keywords
