Introduction

Currently, electromagnetic shields are important objects of scientific and technological development, due to the urgency of solving the problems of ensuring electromagnetic compatibility of electronic equipment, as well as protecting a person from electromagnetic radiation impact. One of the main requirements for the characteristics of currently developed electromagnetic shields is a high electromagnetic radiation attenuation value (more than 30 dB) and a low value of electromagnetic radiation reflection coefficient (less than -5 dB). These requirements are due to the necessity of eliminating the occurrence of situations in which the electromagnetic shield during its using becomes a source of secondary (re-reflected) electromagnetic radiation that affects unshielded objects located near it. Compliance with these requirements can be ensured only in the case of the manufacture of electromagnetic shields in the form of heterogeneous media containing electrically conductive materials. By the latter, it is customary to understand media, which are a set of elements characterized by various electrophysical properties, and in some cases geometric properties. In this regard, electromagnetic shields in the form of heterogeneous media include multilayer shields, as well as shields whose surface is geometrically inhomogeneous (having roughness and / or gaps). The second of these shields are more promising from the point of view of development and research due to the fact that they are characterized by lower weight and size parameters compared to the first. The electromagnetic radiation reflection coefficient and attenuation of such shields, as a rule, depend on the parameters of the geometric inhomogeneities of their surfaces (roughness height, diameter and depth of the slots).

The authors set a goal, which was to establish the influence of the roughness height and the diameter of the slots of the surfaces of electromagnetic shields on the processes of their interaction with electromagnetic waves, the length of which significantly exceeds the parameters of these inhomogeneities. Such processes determine the electromagnetic radiation reflection coefficient and attenuation of the shields. To achieve this goal, the following tasks were solved:

1) an approach for modeling the processes of electromagnetic radiation interaction with the shields in the form of heterogeneous media has been developed;

2) the electromagnetic shields as objects of study have been justified;

3) the initial and boundary conditions for modeling the processes of electromagnetic radiation interaction with the shields under investigation have been determined;

4) modeling of the processes of electromagnetic radiation interaction with the shields under investigation has been  performed depending on the diameter of the slits and the roughness parameters of their surfaces.

The experiment methodology

For the numerical simulation of the electromagnetic shields in the form of heterogeneous media, as well as modeling the processes of electromagnetic radiation interaction with such shields, the COMSOL Multiphysics 3.5 software package was used. Modeling was implemented based on the following approach proposed by the authors.

1. When modeling the electromagnetic shields, a through counting scheme was used without explicitly distinguishing the interface between adjacent media. The possibility of this principle following is due to the fact that the continuity condition for the total current is valid in each section of a layered medium [1].

2. Discretization of electromagnetic radiation propagation medium and the location of the shield interacting with this radiation was performed in such a way that the nodes of the boundaries of the finite elements of the resulting mesh simultaneously belong to media with different electrophysical properties. This is necessary so that the condition of equality of the total currents and the condition of equality of charge flows are satisfied at the interface between the media. Moreover, during the calculation of the electric field strength at the boundaries of the finite elements of the grid (Е_х) it must be taken into account that E_x(x) experiences a discontinuity of a function of the first kind (i.e., a discontinuity of the electromagnetic field) due to the fact that E_x1 ≠ E_x2.

Since E_x(x) is a piecewise smooth and piecewise differentiable function, i. e., it has finite one-sided derivatives E'_x+(x) и E'_x–(x), then at the points of discontinuity x_i the following conditions are satisfied:

,

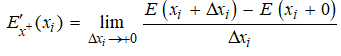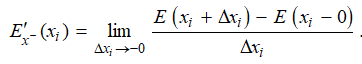
Based on the Dirichlet theorem, the function E(x) at some discontinuity point ξ can be represented as follows:

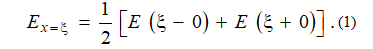
At the interface between media with different electrophysical properties, a double electric layer (DEL) is always formed, the structure of which, as a rule, is unknown, but it has a significant effect on electrokinetic phenomena. It is important to note that in reality the function E(x), which is characteristic of DEL, changes continuously, therefore equation (1) is valid for the case when the thickness of the DEL, i.e., the thickness of the interface, is much smaller than the size of each of the homogeneous elements (layers) of the heterogeneous environment.

If the thickness of the DEL is much smaller than the dimensions of each of the homogeneous elements (layers) of the inhomogeneous medium, then equation (1) can also be obtained and justified on the basis of the condition for a linear change in E(x) in the region of the DEL. The thickness of the DEL depends on the kind of contacting substances and can be tens of angstroms. According to modern concepts, the outer lining of a DEL consists of two parts: the first is formed by ions closely attracted to the surface of one of the elements of an inhomogeneous medium obtained after its discretization (a “dense” or “Helmholtz” layer with a thickness h), and the second by ions located at distances from this surface, exceeding the radius of the ion, and the number of these ions decreases with distance from the interface (“diffuse layer”). The potential in the dense and diffuse parts of the DEL is distributed according to the exponential law [2], that is, the linearity condition E(x) is violated. However, if the thickness of the DES is much smaller than the size of each of the homogeneous elements (layers) of the inhomogeneous medium, then E(x) can be expanded in a power series and, therefore, it can be considered approximately linearly. This allows us to conclude that condition (1) and the stated principle of modeling electromagnetic screens in the form of inhomogeneous media are valid. 

3. When modeling the processes of electromagnetic radiation interaction with electromagnetic radiation, electromagnetic waves in the form of soliton-like signals are used. The rationality of following the stated principle is due to the fact that the penetration depth of such signals in complex environments is higher than other signals currently used in modeling (rectangular, sawtooth, etc.). This is due to the fact that soliton-like signals are less prone to “noise” arising at the interfaces between homogeneous elements (layers) of an inhomogeneous medium. Soliton-like signals are described by the following expressions [3,4]:

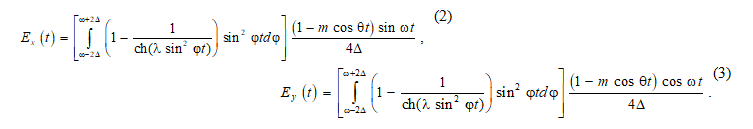
Figure 1 presents the graphical dependencies corresponding to the above expressions and showing the forms of soliton-like signals in the horizontal and vertical planes [2].

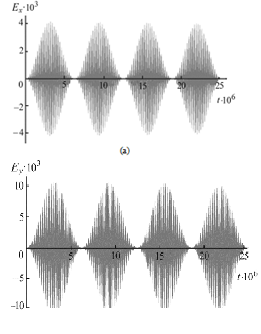
Figure 1: Form of a soliton-like signal in horizontal (a)and vertical (b) planes.

The broadening of the spectral lines is due to the non-stationary process of interaction of the radiating atom with the particles surrounding it – other atoms and molecules, ions and electrons. Therefore, functions of the form (2) and (3) continuously fill the frequency range ω – 2Δ ≤ ω ≤ ω + 2Δ, and it takes some time to establish the signal (transient). It is easy to verify that E_x(t), E_y(t) and their time derivatives satisfy the necessary matching conditions, since they take values equal to zero in the case of pulse propagation in a medium with zero initial conditions [5].

It should also be noted that the wave group is a kind of oscillatory circuit with distributed parameters, in which forced oscillations are not established immediately, but lichens after some time of the appearance of external EMF [6]. After the pulse reaches its maximum value, it monotonically decreases to zero, therefore, in formulas (2) and (3), the authors used the hyperbolic cosine of the harmonic function.

The following electromagnetic shields were selected as objects of study:

– shields based on silver, the surfaces of which are rough (shields 1);

– shields in the form of copper plates, the surfaces of which have slots (shields 2).

The choice of these materials is due to their widespread use at present for the manufacture of electromagnetic shields. In particular, silver coatings, due to their high conductivity and good adhesive properties, are used for electromagnetic shielding of cases and assemblies of high-precision electronic equipment, and copper and copper-containing plates due to their low cost compared to other metal materials in the process of electromagnetic shielding of rooms. 

Results and their discussion

During the simulation, it was assumed that the process of changing the electromagnetic field strength in the area of the screens is described by the following expression:

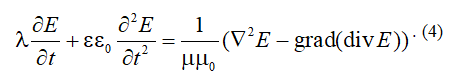
The initial conditions are described using the following expressions:

E(t) was determined according to formulas (2) and (3) with the following parameters: ω = 10¹⁴ s^–1, Δ = 10⁴ s^–1, λ = 10¹⁵ m, θ = 10⁶, m = 1. The values of the integrals were calculated approximately using the Simpson formula. Otherwise, at each iteration it will be necessary to calculate the integrals (2), (3), due to which the calculation time will increase significantly.

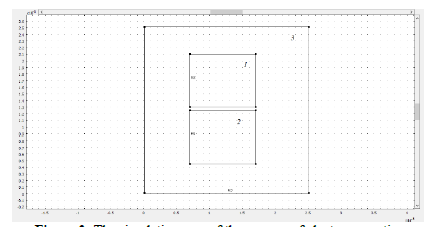
Figures 2 and 3 show the areas in which the process of interaction of electromagnetic radiation with the selected shields was simulated.

Figure 2: The area of modeling the process of electromagnetic radiation interaction with the shield 1: 1– silver; 2 – air medium.

Figure 3: The simulation area of theprocess of electromagnetic radiation interaction with the shield 2: 1, 2:fragments of a copper plate; 3-air medium.

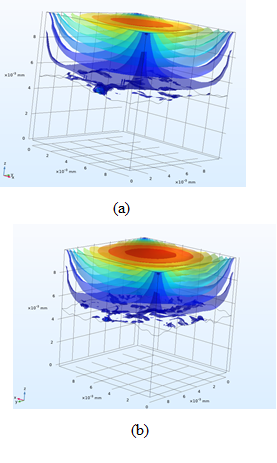
The simulation results of electromagnetic radiation interaction with the shield 1 are presented in Figure 4. The animated simulation result of electromagnetic radiation interaction with the shield 1 is available for viewing by reference https://youtu.be/_Rh2dRbqKpg.

From Figure 4 it follows that the greatest intensity of the electromagnetic field interacting with the shields 1 is observed at the points located in the recesses and at the tops of the roughnesses of their surface. In this case, the tension at the points located in the recesses of the surface is higher than at the points located on the tops of its roughness.

Figure 4: Distributions at time moment t = 4∙10–13s of electromagnetic field strength in the area of the shield 1 location atvarious values of the coefficients of the function used to describethe roughness of its surface: a – b= 2, n = 20; b – b = 1.8, n = 15.

Figure 5: Distributions at time momentt = 10–13 sof electromagnetic field strength in the area of theshield 1 location at adiameter of its slots 500 nm (a), 2μm (b), 4 μm (c), 6 μm(d).

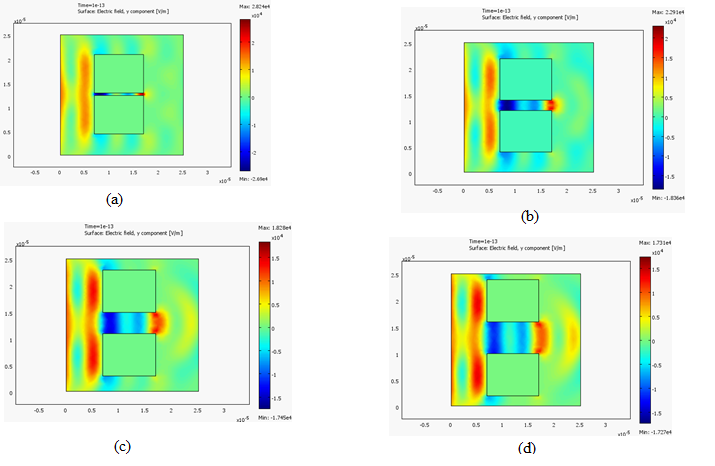
The simulation results of electromagnetic radiation interaction with the shields 2 are presented in Figure 5. The animated simulation result of electromagnetic radiation interaction with the shields 2 is available for viewing by reference

https://www.youtube.com/playlist?list=PLt1iDS0NcZFL4T8_eq2N80qVYvzRrm3nK.

From Figure 5 it follows that an increase in the slots diameter of the shields 2 leads to an increase in the propagation distance through these slots of the electromagnetic field interacting with such shields. The highest electromagnetic field intensity was recorded at the points of the boundaries of the slots lying on the front line of the electromagnetic field and the most distant from the source of this field. It was established that the magnitude of the electromagnetic field strength at these points doesn’t depend on the diameter of the investigated shields slots if the value of this diameter varies from 500 nm to 6 μm.

According to Blokhintsev DI [7], to illustrate the uncertainty relation, the diffraction of an ensemble of particles with a given momentum from a slot in the shield is considered. It was assumed that the wavelength and, at the same time, the total momentum of the particle don’t change during diffraction. In this paper, it is noted that with a decrease in the depth of the slot, the nature of the wave field behind the shield is much more complicated, because the field, when the electromagnetic wavelength is much less than the diameter of the slot, can no longer be characterized by certain values of the wavelength.

In the case of the simulation performed by the authors, the length of electromagnetic waves is much larger than the slots diameter. Based on the evaluation of the simulation results, it was determined that the diffraction length of electromagnetic waves can increase. Moreover, it is determined not only by the slots diameter, but also by its depth. The wave packet in quantum mechanics for non-monochromatic waves, as noted in Quantum Mechanics [7], doesn’t satisfy the matching conditions. In application packages known to the authors for solving electrodynamic problems, the matching conditions are also not considered and not taken into account. Numerical simulation in the presence of strong discontinuities in the electromagnetic field is in this case an incorrect task.

Conclusions

1. The proposed approach, unlike analogues, is characterized by the following features:

– based on the use of electromagnetic waves in the form of soliton-like signals, which take into account the temporal dispersion of electrical induction (taking into account the unsteady broadening of their spectral lines and integration over the continuous spectrum), which eliminates the need to neglect spatial derivatives, as well as use spatial nonlocal relations to take into account the influence of surface charge, surface current and spatial dispersion of electric induction at the interfaces of adjacent media;

– based on the creation of an “unsharp” interface between adjacent media using the Dirichlet theorem for piecewise smooth functions and with the condition of continuity of the total current.

2. Based on the simulation results carried out using the proposed approach, we can conclude that the maximum electromagnetic field interacting with the shields whose surface is geometrically inhomogeneous is observed at the points of this surface that are most distant from the electromagnetic source (in the recesses). This allows us to conclude that the development of technologies for heterogenizing the surfaces of electromagnetic shields is promising in order to reduce the values of their electromagnetic radiation reflection coefficients while maintaining the attenuation values.

Foundation

This work was supported by the Belarusian Republican Foundation for Basic Research, project No. F19-096.

References

1. Samarskii A.A (1989) Theory of Difference Schemes. Nauka, Moscow. (In Russian)
2. Evans DF and Matesich MA (1977) Measurement Methods in Electrochemistry, Yeager E and Salkind AJ (eds.,) 2: 10-69. Mir, Moscow. (In Russian)
3. Antonov VF, Chernysh AM, Pasechnik V.I., et al. (2000) Biophysics. Gumanitarnyi Izdatel’skii Tsentr “Vlados”, Moscow Russian.
4. Grinchik NN, Lazuk VI (2016) Soliton-like pulse signal in a medium with strong discontinuities in the electromagnetic field. Part II: Numerical modeling Heat and mass transfer-2016: collection of scientific papers, 2016, 189-196.
5. Grinchik NN, Andrejev VG, Zayats GM and Grinchik YN. (2018) Non-Monochromatic electromagnetic radiation of inhomogeneous media. JEMAA 2: 13-33.  https://doi.org/10.4236/jemaa.2018.102002
6. Kalashnikov SG (1985) Electricity. Nauka, Moscow. (In Russian)
7. Blokhintsev DI (2015) Quantum Mechanics: Lectures on Selected Issues (2nd edtn), Lenand, Moscow. (In Russian) 

Corresponding author: Boiprav OV, Educational Institution “Belarusian State University of Informatics and Radioelectronics”, Minsk, Belarus, E-mail: boiprav@tut.by

Citation: Aliseyko MA, Boiprav OV, Grinchik NN, Tarasevich AV. Modeling the interaction of solit-like pulse signals with electromagnetic shields in the form of heterogeneous media (2020) Edelweiss Chem Sci J 3: 1-5.

Keywords

Artificial intelligence, Information and communications technology, Crystallography, Out-of-scope prediction.