Introduction

Under equivalent experimental conditions, low frequency words are better recognized than high frequency words. This phenomenon is known as the word frequency effect in recognition memory [1]. The word frequency effect is also known as the mirror effect [2] due to the shape of the response distribution.

The frequency of use (familiarity) is very relevant in the neurological rehabilitation of language and memory because, according to our general hypothesis in this work, the recognition of the most frequent words provides more false alarms than the recognition of infrequent words.

In this sense, the present work represents a formal theoretical model, and a methodology for the generation of techniques for the rehabilitation of episodic and semantic memory. The words on reaction times, in this context, are consistent with greater resources of attention in the processing of less frequent words, but this is not the current objective of this work.

This topic is relevant because word frequency is the best predictor of performance in recognition memory tasks [3]. This paper presents a formal model of multi-level responses obtained by the use of a rating scale and their Receiver Operating Characteristic (ROC) data [4,5].

The first objective (or general hypothesis) was to obtain the responses to a recognition memory task and the scores on the rating scale. These responses can be empirically obtained using the formal distribution of the stimuli used in the experiment [6]. Thus, the responses would depend on:                    

where, d is the discrimination (after correcting for deviation τ), is the signal distribution, and  is the noise distribution [7]. The discrimination index in equation 1 can be re-written as a logit model:              

where the index d in the equation 1 acquires a value of the logit function: Y represents yes answers to signal S, and c is replaced by the observer´s criterion. 

The equivalent equation for noise is as follows:  

where, S is replaced by N. 

From the integration of equations 1, 2 and 3 we obtain: 

where, the participants response, at least under criterion c, represents a threshold in the sensorial continuum. Thus, equation 4 can be transformed into:

where, two levels of response are taken into account. One level is derived from variable X, (or in Signal Detection Theory (SDT), and the other c from criterion (criterion or threshold in SDT). This procedure can be generalized by the successive replacement of elements in order to obtain an equivalent general linear model [8,9].

where, indicates the probability of discrimination that depends on the value of parameter αin the variable X as well as on the parameter β.

When all possible responses j in a rating scale are generalized, the following model is obtained:

where, j is a set of sorted values [7] that can represent the subjects responses for a given value of X. This procedure provides a general model to obtain the responses [9], or subjective rating scales [10]. 

The mathematical models, presented previously, allow to elaborate formal hypotheses, as well as to generalize our results for the elaboration of multiple clinical materials for neurological rehabilitation affected by the word frequency. 

Our second objective (or general hypothesis) was to include the responses in the model, which were standardized (z) through Receiver Operating Characteristic (z-ROC) data. We obtained the values for intercept and slope, which are the parameters of a quantitative model, where the slope is obtained by calculating the ratio between the standard deviations of noise and signal (σn/σs) and the intercept is the difference between the average estimations of signal and noise divided by the standard deviations of signal (µs-µn)/σsn) [11]. The intercept is similar to the equation 1.

The ROC distribution described above allows continuous and threshold distributions to be detected [10]. We conceptualize continuity as described in Yonelinas and Park. A theory based on continuity is congruent with the classic model of SDT [12]. Nevertheless, empirical threshold models provide a better description of changes in memory level [12]. Hypothetically, these changes are due to sudden changes in acquisition tendencies due to learning or memorizing. For this reason, despite SDT being based on the concept of continuity, we assumed that a z-ROC model would allow us to empirically use both continuous and threshold data and thus obtain an empirical and unified model of formal analysis. 

Given the two objectives described above, we investigated data continuity (non-existence of a threshold) in the z-ROC data [13]. Data continuity has been investigated in experiments using hypotheses based on familiarity (e.g., through the presentation of very frequent stimuli) or on the strength of memory prints, or in experiments using brief exposure times to stimuli or in experiments on implicit memory [14]. The notion of a sensory threshold and mathematical models to explain the gradual nature of observed functions [6]. We hypothesized that nearly linear continuous z-ROC data would be obtained in a recognition memory task using HF word lists. 

In contrast, we hypothesized that z-ROC data would be discontinuous (non-linear). This hypothesis would be plausible in experimental designs that allow sufficient conscious processing time (e.g., >500 ms per word) to produce learning [14]. 

Our experimental hypothesis assumed that there would be more false alarms in HF word recognition memory and fewer false alarms in LF word recognition memory. This hypothetical outcome would be detected via the different trends in the distribution of the mathematical functions for each z-ROC data. In effect, the z-ROC data would show that LF stimuli would cause breaks in continuity in the trend, thereby producing threshold effects (a U-shaped z-ROC data) suppress, whereas HF stimuli would be associated with z-ROC data resembling straight lines.

Material and Methods 

Experiment 1: Laboratory

Participants: The experiment included 48 undergraduate students Spanish, monolinguals who participated voluntarily (21 men and 27 women; age range: 18-26) from the University of Malaga (Spain). None of the participants had any disease or disorder that could have affected the experiment. Its control is carried out through self-report and training test.

Measures: We used frequency dictionaries to assign 80 words, appendix 1, 40 Low Frequency (LF) words and 40 High Frequency (HF) words) to one of two experimental conditions [15,16]. The selected words contained 3 to 5 letters and 1 or 2 syllables to control for length. Each set of 40 words was divided into 20 words randomly assigned as signal words and 20 as noise words. All other features of the experiment were made constant to avoid affecting the magnitude of the frequency effect.

Procedure: E-prime was used to serially present the two word lists, one word at a time [17]. The order of presentation of the words in each list was randomized for each individual trial and the order of experimental conditions was counter-balanced for each participant, thus controlling for primacy and recency effects. The monitors used, distance to monitor, viewing angle, and researchers present were the same for all participants. The monitor is a Acer, 15, AL 506 model. The visual distance to the monitor is 50 cm, and the visual angle is 35º. Verdana letters of size 14 were used.

All participants underwent training before the trials until they were familiar with the task. The task consisted in the application of a discrimination paradigm in recognition memory based on the SDT model, with YES-NO, plus rating scale answers. Each participant memorized a list of 20 words in a serial manner, after which said words were randomly mixed with 20 new words. That is, a list of 40 words. The participants had to answer YES or NO to each word presented indicating if the target word had been presented previously (YES answer) or if it was a new word (NO answer). The words were presented randomly for each participant. The participants answered verbally and one researcher wrote the answer YES- NO. In summary, the recognition task consisted in the participants indicating whether 20 previously presented words were present or not in a new list of words that included the 20 target words (signal) and 20 new words (noise). The participants gave their responses using an STD-based yes/no format and a 5-point Likert-type scale ranging from 5 (very high confidence in their own answers) to 1 (very low confidence in their answer). Each word was presented on screen for 500 ms, and with two seconds of interval between stimuli. To control for primacy and recency effects in short-term memory, there was a 40-s interval between presentation and recognition. The participants were asked to respond as quickly as possible.

 Analysis: A one-factor analysis of variance (ANOVA) was conducted to determine the hits and false alarm rates in each experimental condition, HF and LF. The corresponding z-ROC data were calculated.

 Results 

Significant differences were found between HF and LF words in the number of false alarms: ANOVA, F (1, 46) = 4.13, MCE. = 2.34, p = 0.003. The Cohen effect sizes were 0.6. 

The ANOVA with respect to other variables of SDT model was not significant. An asymmetric distribution was found in the z-ROC data in relation to the minor diagonal. Maximum discrimination values for HF words and LF words were d= 0.12 and d = 0.36, respectively. In addition, the G test was applied, test showed that the differences were statistically significant, G = 3.75, p = 0.01. 

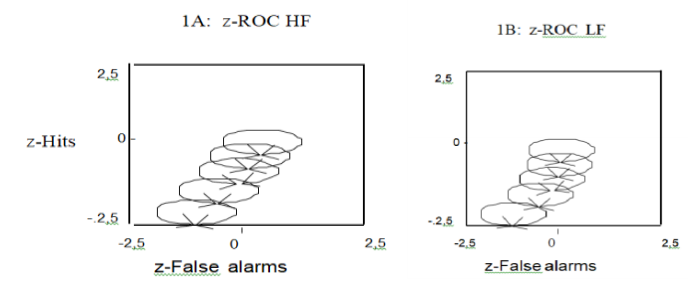
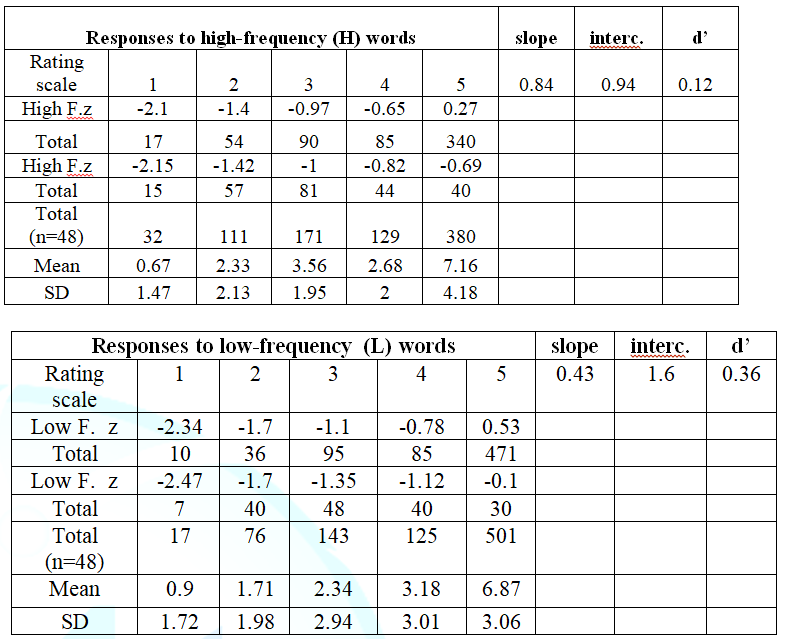
There is a significant effect of the word, top-down processing on false alarms, versus non-significant processing based on the comparison between the number of syllables of the words (Table 1). 

Table 1: Accumulated proportions of hits signal and noise: Hits, false alarms, correct rejections, and incorrect rejections. 

Two different z-ROC data were identified: a relatively straight data for HF words and a relatively U-shaped data for LF words (Figures 1A and 1B, respectively). The slope was 0.76 and 0.43 for HF words and LF words, respectively, and the intercept was 0.94 for HF words and 1.60 for LF words, respectively. The hit rate was higher for LF words than for HF words, whereas the false alarm rate was lower for LF words than for HF words (mirror effect). Table 1 shows the accumulated frequency of hits and false alarms for each point on the rating scale in the two frequency conditions and the corresponding z-ROC values (Figure 1 and Table 2).

Figure 1: Laboratory experiment. Representation of data and z-ROC data (A and B) for high- and low-frequency words. 

Table 2: Accumulated frequency of hits and false alarms for each point in the rating scale in the two frequency conditions, and z-ROC values (laboratory). 

Experiment 2: Class-room

Experiment 1 was replicated in a natural setting to test whether the frequency effect occurred in the conditions in which academic learning usually takes place. We expect differences in the results due to contextual variables, but not in reference to the general hypothesis of this work. The only differences between the two experiments were the setting. 

The experiment 2 was done during the regular class schedule, the number of participants (15 men and 33 women, age range: 18-26) from the University of Malaga (Spain). None of the participants had any disease or disorder that could have affected the experiment. The 20 signal words were first presented in a DIN A4 sheet for 6 seconds, which was proportional to the presentation time in Experiment 1. The 40 words (20 signal and 20 noise) were then presented in the same format for 12 seconds. The participants were asked to write, adjacent to each word, whether or not they recognised it and also completed the 5-point Likert-type rating scale. 

Results

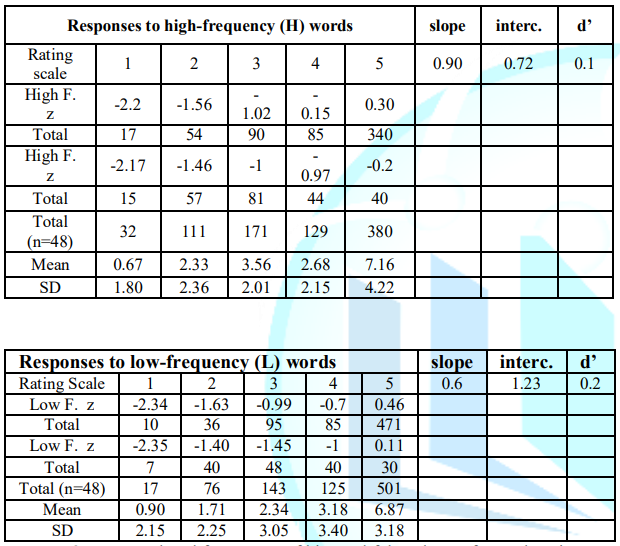
Significant differences were too found between HF and LF words in the number of false alarms: ANOVA, F (1, 46) = 3.71, MCE. = 12, 36, p = 0. 01. The Cohen effect sizes were 0.45. Maximum discrimination values for HF words and LF words were d= 0.10 and d = 0.20, respectively. Gourevitch and Galanters test showed that the differences were statistically significant, G = 2.05, p = 0.04.

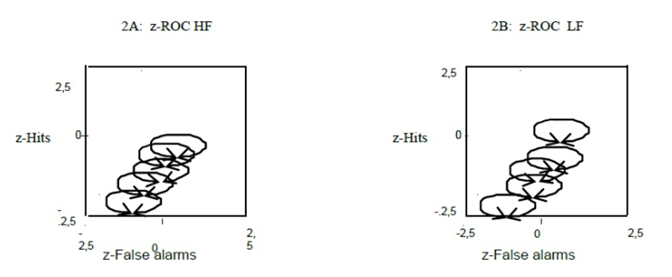
As in experiment 1, the z-ROC data for HF words was relatively straight, whereas for LF words it was relatively U-shaped (Figures 2A and 2B, respectively). The hit rate was higher for LF words than for HF words, whereas the false alarm rate was lower for LF words than for HF words (mirror effect). The slope was 0.90 and 0.57 for HF words and LF words, respectively, and the intercepts were 0.72 and 1.23 for HF words and LF words, respectively (Figure 2 and Table 3).

Figure 2: Class-room experiment. Representation of data and z-ROC data (A and B) for high- and low-frequency words.

Table 3: Accumulated frequency of hits and false alarms for each point in the rating scale in the two frequency conditions, and z-ROC values (class-room).

In summary, the ANOVA showed that there were no statistically significant differences between laboratory and class-room settings or between some of the basic SDT parameters (hits and false alarms, ROC data, d, and G test) used to improve the statistical power of the ANOVA. The results of the experiment in the class-room validate the laboratory experiment. But different contextual variables in the class-room context produce more intra experimental variability (Table 3). 

Discussion

The trend of the data is observed in the ROC data, tables and figures previously mentioned. The results of both experiments confirm the hypothesis that LF words are better discriminated than HF words and are recognised in a qualitatively different manner. A familiarity process is indicated by the linear shape of the z-ROC data and HF words. The other hand, a familiarity process is indicated by the straight line with a slope which is nearer to one Hence, we assume that LF words are associated with recollection processes, which is in agreement with model initially proposed by Yonelinas and Park, whereas familiarity processes are associated with classic SDT theory [12].

The differences found between HF and LF words in their d values and intercepts aim in the same direction; together with the formula posed by Cohen [19], they estimate power and test size, but Cohen effect sizes was greater in the laboratory experiment. The slope values inversely correlated with d and intercept. These findings confirm the existence of two different processes: one for HF words and another for LF words. Furthermore, the hit and false alarm rates further serve to differentiate between familiarity and threshold response models, as described by Wickens. 

A possible explanation for these findings is to assume that highly familiar stimuli fit into a continuous model, as suggested by Bröder & Schütz [20]. Nevertheless, these authors prefer the term strength or evidence [20] because the term strength has fewer theoretical implications. Strength is the term traditionally used in word memory studies based on SDT and the ROC data paradigm, whereas recall is the term suggested by Yonelinas and Park. Recall would be represented by a high threshold. The model we propose is consistent with continuous models, such as SDT, that assume that decisions are based on Bayesian statistics [21]. Signal Detection Theory uses a priori probabilities of signal and noise as a technique to analyse responses (signal-noise and hits-false alarms). This approach is also suitable to analyse classified non-randomized words [22].

Our model suggests that word frequency is coded in the semantic structure of language and that this coding contributes to the frequency effect observed in word recognition experiments. Thus, the ideal category (signal) for rapid cognitive learning would be LF words [23] with a high semantic load (e.g., LF words with complex or deep meanings). 

The previous suggestion can be generalized to heuristic non-linguistic models [24]. We also identified a double dissociation between stimulus meaning and word frequency effect, which suggests future lines of research. Our results support the possibility that HF words may place higher demands on control processes, although these words are in turn masked and negatively affected by their higher frequency [25]. It has been found that naming latencies for homophones are indistinguishable from those for non-homophone controls matched on word-specific frequency [26]. In a different setting, these results support our initial hypothesis on the frequency effect extended not only to the setting of recognition memory, but also to the setting of speech production. 

Others researchers have also suggested a shared simple and dual processing model [27], but only as an experimental model in a lexical context in which word frequency affects the connections between the orthographic lexicon and phonologic lexicon [28]. These findings point to new directions in research and in the formalization of models. 

A general memory model should include the distribution of all the possible responses obtained [10] and their assessment via suitable mathematical distributions (e.g., ROC data), which would allow the results (or responses) of other models to be included in the general memory model. The substantive theory would be based on a general memory model that uses classified stimuli (according to frequency of use in this study); its results would oscillate on a continuum between two points: random recognition and fully aware recognition. This continuum is affected by numerous complex variables, many of which remain to be identified. Is an example of these types of variable the additive effects of stimulus quality and word frequency [29]. 

However, future research we have to considerer the relationship between frequency and transparency of the words, for example: the interaction between transparency and base frequency comes from targets that adequately represent the entire spectrum of transparency [30]. It should be noted that the transparency by base frequency interaction is consistent with a distributed connectionist framework [31]. Another relevant variable is the time in years, effectively the variable frequency changes in relation to the time in different ways [32] or the colour vision on the Alzheimer deficiencies in Alzheimers disease [33] and in medical decision methods [34].

References

*Corresponding author 

Manuel Pelegrina del Río, Department of Psychobiology and Methodology, Faculty of psychology, Malaga university, Malaga, Spain, Tel: 952132538, E-mail: pelegrina@uma.es

Citation

Pelegrina del Río M, Ruiz AW, Fernandez MCM and Fernández AP. ROC modelling data of the word frequency effect: A formal model of visual word recognition (2019) Neurophysio & Rehab 2: 1-5

Keywords

Modelling, Memory, Frequency, Words