Research Article :
Nerve impulse has been
simulated as an ion–acoustic breather containing the internal FPU recurrence
spectrum. The strong electrolyte of intracellular fluid is interpreted as dense
plasma where electroacoustic solitons can propagate. The dynamics of sodium ion
concentration is described by the sine-Gordon equation while the dynamics of
proton concentration is done by the Korteweg de Vries equation. The system of
these coupled equations has a breather solution having an intrinsic structure
with the Fermi–Pasta–Ulam recurrence. Its spectrum possesses a dynamic memory
for the initial conditions of its modes. Such breathers can be generated in
firing process of a neuron. The information capacity of each breather can reach
1014 bits. Traditionally, the electrical
activity of a single neuron is described within the framework of the
Hodgkin-Huxley model [1], where, in accordance with the Hartley formula, the
information capacity of a single spike is bit. In other words, a neuron is
considered as a system with two states, and all the complexity of a brains
ability to process information is explained by the presence of numerous
parallel processing paths. However researches have reported correlations
between learning and changes in ribonucleic acid (RNA) and protein in neurons
[2]. These data supported a hypothesis [3] that a single neuron, based on the
number of triplets existing in its RNA molecule can sustain an information
capacity up to bits.
The purpose of this paper is to
develop a neuronal model based on the complex FPU recurrence spectrum,
interpreted as an information carrier. The FPU recurrence phenomenon was first
reported in 1955 [4] as a result of a computer simulation of the oscillatory
dynamics in a chain of non-linearly coupled vibrators with fixed ends. In contrast
to logical expectations, this system did not have a tendency toward
equipartition of energy among its degrees of freedom. Instead of this, a
periodical recurrence of the initial perturbation energy spectrum was observed.
Later [5], it was established that the FPU phenomenon has two types of
recurrence: simple and complex. In a simple recurrence, an almost perfect
periodic return of energy spectra is observed in the system, whereas in a
complex version, the periods not stable and Fourier modes exhibit complex
sharing and regrouping of energy. This interesting behavior of the
FPU chain stimulated a number of investigations of the system [6,7,8,9]. The
first theoretical description of the problem was done by Zabusky and Kruskal
[10], who showed that FPU recurrence can be described by the Korteweg-de Vries
(KdV) equation with periodic initial conditions. Another team of researchers, Yuen and Lake, were able to
describe FPU recurrence within the framework of the Nonlinear Schrodinger
Equation (NLS) with periodic boundary conditions [11]. Same authors reported
about very interesting property of the FPU recurrence to "remember"
the initial conditions for the active modes of its spectrum, reproducing them
periodically in the FPU spectrum. In another study of the FPU problem [12], it
was proposed that the exchange of energy between modes of the system is
connected with a transition to strong stochastisity. In discussing early
investigations of FPU recurrence, it is necessary to emphasize that the
original vibrators chain had fixed ends [4]. But with open ends, the chain also
can represent a theoretically interesting autonomous distributed system,
responsive to initial perturbations. As a first step of our study we tried to
consider neural activity using a plasma approach. We shall consider a neuron as a
volume containing the strong electrolyte of intracellular fluid in which RNA
molecule plays the role of neural information carrier. Additionally we assume
that all potassium ions are electrically neutralized by forming ionic couples
with hydroxyl groups that provides an overbalance of protons in the
electrolyte of the neuronal intracellular fluid. Such assumptions allow us to
analyze the proton dynamics by applying the simplified cluster model of the
seawater strong electrolyte suggested by Frank and Wen [15]. In this model,
every sodium ion is surrounded by ionic atmosphere consisting of four water
molecules and every chlorine ion has two water molecules in its atmosphere (Figure
1). Since the
duration of a nerve impulse constitutes units of milliseconds [18] we can
formally evaluate the single spike information capacity applying Kotelnikovs
theorem [19] as follows: Here, t = S/cs, where S = L/sinais
the soliton length, ais the resonator spirality angle, cs = 104 m×s–1, S = 10 m,
L = 10 cm, and sina = 0.1. The next step is
to show how this high frequency signal can be embedded into the structure of
the action potential. For this purpose, we shall consider a neuron membrane as
a liquid crystal containing a lipid bilayer
[20] (Figure 1). Accounting the distance between the lipid molecules in the
membrane layer and the distance between sodium ions in the chain (Figure 1) to
be about 4.7 A [16,21], we can suggest the following mechanism of interaction
between high frequency proton concentration wave and the ionic wave of the
action potential. Consider the
sodium chain shifted at a distance U relative to the equilibrium positions of
the lipid molecules of the membrane lower layer (Figure 1). Such a picture
allows applying the approach developed by Frenkel and Kontorova [22] for the
analysis of dislocations dynamics in crystals. We define potential
effecting n-th sodium ion from the immovable chain of lipid molecules in the neuron
membrane layer (Figure 1) as: Where - is the distance
between neighboring lipid molecules in the membrane layer, - relative
position of the lipid molecule. In this case the
dynamics of the sodium ion shift can be described by the following equation
[23]: Where Now using the
continuum approximation and introducing
a function proportional to the modulation of the sodium ion density in a form: We obtain the sine-Gordon equation: The dimension of
a neuron will define the
boundary conditions for Eq. (10) by analogy with a long transmission line
open on both ends, which was used for simulation of the Josephson junction
dynamics [25]:As shown by
Fulton [25] for chains with limited length described by the sine-Gordon
equation there exists an energy exchange between soliton and plasma solution.
This type of Eq. (10) solution represents in the limit the standing
waves which are close to the knoidal waves of the KdV [26]. These properties of
Eq. (10) give an opportunity to apply the experimentally established plasma
phenomenon of locking high frequency electric field by the low density plasma
regions [27]. Within the framework of this approach we can interpret a spike as
a locker of high frequency proton concentration waves within the body of the
sodium ion concentration waves, because the strong electrolyte of the neuron
intracellular fluid can be considered as a dense plasma. So the nerve spike
forming process can be described by the system of coupled sine-Gordon and KdV
equations: where, < 1 - are
the coefficients of interaction between sodium ion concentration waves and
proton ones. In accordance
with the results of Ikezi paper [27], in which a similar pair of equations was
studied, the solution of the system (13) represents a soliton with internal
oscillatory structure. Parametrical coupling of equations in (13) provides an
effective energy exchange [13]. We looked for the systems (13) solution having
the following considerations. Since periodical initial conditions imposed on
the KdV equation resulted in the model of Zabusky and Kruskal in forming the
FPU solution we considered the influence of intermittent KdV solitons on the SG
equation as a perturbing factor. Soliton of the SG equation captures the modes
of this external influence. The number of captured modes is connected with the
asymptotic phase shift [28]. To get the SG perturbed solution it is necessary
to highlight the perturbation at the background of the SG soliton: and to
linearize the obtained equation over y. Therefore, we get an equation with a “dispersing” potential: y
=f(x)exp(iwt). For the SG
equation looks as
follows [28]. where , function yields the
following equation
In (15) there was carried out the Lorentz transform for the coordinat system
moving at the solitons velocity. From here for f(x) we obtain. The solutions of (16) consist
of one bound state and a continues spectrum [28]. As it follows from (18)
due to the motionless soliton of the SG equation the KdV solitons phase shifts
in asymptotic for a magnitude . If to introduce a chain length as it is possible
to get a density state as The most important
feature of functions (17) and (18) is that they being the own functions of self-conjugated
operator (16), form a full multitude - basis in the space of functions of
variable x. This multitude represents a natural basis for the interpretation of
the solution perturbations as a soliton. In this case the modes of continues
spectrum reflect the soliton form changing and the “emission” as well. The
conditions of orthoganality and fullness have the following expression [28]. As it follows from (21)
and (22) they can be used for expanding any arbitrary perturbation and their
contributions into the energy separate. where is the soliton
energy, - “mass of
peace ” of the soliton in the SG equation [28]. In the simplest case the
solution of the couple (13) can be given in a form of the SG breather, that
intrinsic oscillatory degrees of freedom represent the FPU recurrence of the
Zabusky and Kruskal model [10]. Besides, the summary energy of the FPU modes in
a form of the Fourier sequence and the energy of non - equidistant modes
remains constant and a reversible regrouping of energy takes place between
equidistant and non - equidistant spectra of frequencies so representing the
full FPU recurrence. In the equation (24)
the interaction between the energies of equidistant and non -equidistant modes
takes place due to the continues spectrum and the KdV solitons “tails”. As it
can be seen from (24) that is the FPU character depends overwhelmingly on the
peculiarities of the medium, for example, admixtures like will result in changing in space the coefficient w
in the SG equation. If to transfer the FPU scenario on macromolecules like
neural RNA its spectrum characteristics will fully depend on the nitrogen bases
sequence along the molecules. Having the described theoretical basis for the
full FPU recurrence, we consider a physical model for this phenomenon. Developed
model enlarges the existing notion about a neuron as a simple binary cell and
can explain the information processing ability in some insects having only few
neurons. These data supported a hypothesis [3] that a single neuron, based on
the number of triplets existing in its RNA molecule can sustain an information
capacity up to bits. Besides, any
intracellular fluid or electrolyte in organism can probably serve as a medium
for propagating ion – acoustic solitons. Moreover, neurons can be arranged into
local or general associative systems. For complete information visit PDF References 1.
Hodgkin AL and Huxley AF. A quantitative description
of membrane current and its application to conduction and excitation in nerve
(1952) J Physical (Lond) 117: 500-544. https://doi.org/10.1007/BF02459568 2.
Hyden H and E Egyhazi. Changes in RNA content and
base composition in cortical neurons of rats in a learning experiment involving
transfer of handiness (1964) Proc Nat Acad Sci 52: 1030. https://doi.org/10.1073/pnas.52.4.1030 3.
Hyden.H. Biochemical aspects of learning and memory.
in Human Mind, Amsterdam, 29 (1967). 4.
Fermi E, Pasta J and Ulam S. Studies of nonlinear
problems. Los Alamos report LA-1940 in Collected papers of Enrico Fermi (1955)
Chicago Univ Press 2: 978. 5.
Yuen HC and Ferguson WE. Fermi–Pasta–Ulam recurrence
in the two‐space dimensional nonlinear Schrödinger equation (1978) Phys Fluids 22:
2116. https://doi.org/10.1063/1.862122 6.
Ford J and Waters J. Computer Studies of Energy
Sharing and Ergodicity for Nonlinear Oscillator Systems (1963) J Math Phys 4:
1293. https://doi.org/10.1063/1.1703904 7.
Tuck J and Menzel M. The superperiod of the
nonlinear weighted string (FPU) problem (1972) Adv Math 9: 399. https://doi.org/10.1016/0001-8708(72)90024-2 8.
Livi RM, Paladin G, Ruffo S and Vulpiani A. Advances
in Phase Transition and Disordered Systems (1985) Phys Rev A 31: 1039. 9.
Sholl DS and Henry BI. Recurrence times in cubic and
quartic Fermi-Pasta-Ulam chains: A shifted-frequency perturbation treatment
(1991) Phys Rev A 44: 6364. http://dx.doi.org/10.1103/PhysRevA.44.6364 10. Zubusky NJ and MD Kruskal. Interaction of "Solitons" in a
Collision less Plasma and the Recurrence of Initial States (1965) Phys Rev Lett
15: 240. https://doi.org/10.1103/PhysRevLett.15.240 11. Yuen HC and Lake BM. New model for nonlinear gravity waves. Part 1.
Physical model and experimental evidence (1978) Academic Press, New York San Fracisco
London. http://dx.doi.org/10.1017/S0022112078001974 12. Pettini M and M Landolphi. Dynamics of screening in multifractal growth
(1990) Phys Rev A 41: 768. http://dx.doi.org/10.1103/PhysRevA.41.582 13. Berezin AA, Kukushkin Pavel B and Andriankin Erast U. Theoretical
simulation of a coherent coupled electromagnetic wave structure recurrence
induced by the white noise (1988) Physica Scripta 38: 719-720. https://doi.org/10.1088/0031-8949/38/5/011 14. Luck JM and Mehta A. Bouncing ball with a finite restitution: Chattering,
locking, and chaos (1991) Phys Rev E 48: 3988. https://doi.org/10.1103/PhysRevE.48.3988 15. Frank HS and Wen WY. Ion-solvent interaction Structural aspects of
ion-solvent interaction in aqueous solutions: a suggested picture of water
structure (1957) Disc Faraday Soc 24: 133. http://dx.doi.org/10.1039/DF9572400133 16. Skorcheletti VV. Theoretical Electrochemistry (1963) Goshimizdat.
Leningrad. 17. Toda M. Vibration of a Chain with Nonlinear Interaction (1967) Phys Soc
Japan 22: 431. https://doi.org/10.1142/9789814354332_0014 18. Damask AC. Advances in Biological and Medical Physics (1978) Medical
physics V1 Academic Press. 19. Gonorovsky IS. Electronic circuits and signals (1967) Soviet Radio V1. 20. Barnes FS and Chia-lun.J Hu. Nonlinear Electromagnetics (1980) Academic
Press. 21. Americ UB and Kretsel BA. Chemistry of liquid crystals and mesamorphous
polimer systems (1981) Nauka, Moscow. 22. Frenkel JI and Kontorova TA (1938) J Theoret Exp.Phys 8: 89. 23. Davydov AS. Solitons in molecular systems (1988) Naukova Dumka. https://doi.org/10.1088/0031-8949/20/3-4/013 24. Pelinovsky EN (1976) Radiofisica v.XIX n5-6: 883. 25. Fulton TA. Superconductor Applications: SQUIDs and Machines (1977) Plenum
Press, N.Y, USA. 26. Scott AC. Birth of Paradigm.in Solitons in Action (1978) Academic Press,
New York San Fracisco London, UK 307. 27. Ikezi H. Solitons in plasmas (1978) Academic Press, USA. 28. Fogel MB, et al. (1977) Phys Rev B 15: 1578.Electrochemical Approach in Description of a Nerve Impulse
Andrey Berezin, Alexander Shmid
Abstract
Full-Text
Introduction
Neural
activity model
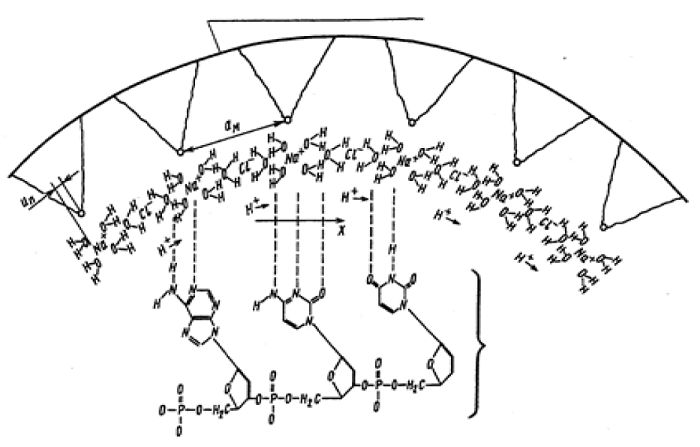
Figure 1: Plasma model of a neuron.
In a spherical volume of a neuron, consider one-dimensional chain of Na+ and
Cl- ions near the lower layer of neuronal membrane as illustrated in Figure 1.
Depolarization of the membrane creates a nonlinear proton concentration wave
due to the "croquet" mechanism of proton transport between water
molecules, suggested by Bernal [16]. The electric potential created by the combined sodium ion and
the chlorine ion and the chlorine ion atmosphere
can be defined within the framework of the Debye-Hukkel theory as a sum of
repelling and attracting parts [16]:![]() - is the
elastic constant for the relative shift of the sodium ions.
- is the
elastic constant for the relative shift of the sodium ions.Conclusion